题目内容
 已知,如图,⊙O2的圆心O2在⊙O1上,且⊙O1与⊙O2的半径均为1,那么阴影部分的面积是
已知,如图,⊙O2的圆心O2在⊙O1上,且⊙O1与⊙O2的半径均为1,那么阴影部分的面积是分析:要求阴影部分的面积就要先求出三角形的面积和弓形的面积.
解答: 解:如图,设两圆相交于点A,B,
解:如图,设两圆相交于点A,B,
阴影部分的面积等于两个等边三角形的面积加上四个弓形的面积.
一个等边三角形的面积=
×1×1×sin60°=
,
弓形的面积等于圆心角为60度的扇形减去等边三角形的面积,
一个弓形的面积=
-
=
-
,
∴阴影部分的面积=2×
+4×(
-
)=
π-
.
 解:如图,设两圆相交于点A,B,
解:如图,设两圆相交于点A,B,阴影部分的面积等于两个等边三角形的面积加上四个弓形的面积.
一个等边三角形的面积=
| 1 |
| 2 |
| ||
| 4 |
弓形的面积等于圆心角为60度的扇形减去等边三角形的面积,
一个弓形的面积=
| 60π×1 |
| 360 |
| ||
| 4 |
| π |
| 6 |
| ||
| 4 |
∴阴影部分的面积=2×
| ||
| 4 |
| π |
| 6 |
| ||
| 4 |
| 2 |
| 3 |
| ||
| 2 |
点评:本题考查了等边三角形的性质和面积公式,扇形的面积公式,弓形的面积求法.

练习册系列答案
相关题目
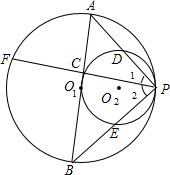 O2交于D、E两点,延长PC交⊙O1于点F.
O2交于D、E两点,延长PC交⊙O1于点F. 已知,如图,⊙O2的圆心O2在⊙O1上,且⊙O1与⊙O2的半径均为1,那么阴影部分的面积是________.
已知,如图,⊙O2的圆心O2在⊙O1上,且⊙O1与⊙O2的半径均为1,那么阴影部分的面积是________.
