题目内容
下列各式计算中,正确的是( )
A. 2a+2=4a B. ﹣2x2+4x2=2x2 C. x+x=x2 D. 2a+3b=5ab
B 【解析】试题分析:A选项不是同类项,无法进行加减法计算;B选项计算正确;C、原式=2x;D选项不是同类项,无法进行加减法计算.故选B.下列说法正确的是( )
A. 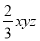 与
与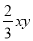 是同类项 B.
是同类项 B. 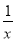 和
和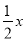 是同类项
是同类项
C. 0.5x3y2与7x2y3是同类项 D. 5m2n与﹣4nm2是同类项
查看答案下列各式中,等号不成立的是( )
A. |﹣4|=4 B. ﹣|4|=|﹣4| C. |﹣4|=|4| D. ﹣|﹣4|=﹣4
查看答案下列式子中,正确的是( )
A. ﹣6<﹣8 B. ﹣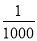 >0 C. ﹣
>0 C. ﹣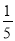 <﹣
<﹣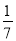 D.
D. 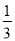 <0.3
<0.3
﹣2007的绝对值是( )
A. ﹣2007 B. ﹣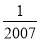 C.
C. 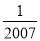 D. 2007
D. 2007
若规定收入为“+”,那么﹣50元表示( )
A.收入了50元
B.支出了50元
C.没有收入也没有支出
D.收入了100元
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 阅读快车系列答案
阅读快车系列答案抛物线y=2x2-3的顶点在( )
A. 第一象限 B. 第二象限 C. x轴上 D. y轴
D 【解析】试题分析:b=0,抛物线的对称轴是y轴,所以顶点在y轴上,故选D.下列函数解析式中,一定为二次函数的是()
A. y=3x?1 B. y=ax2+bx+c
C. s=2t2+2t+1 D. y=x2+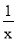
一元二次方程x2﹣2x=0的根是( )
A. x1=0,x2=﹣2 B. x1=1,x2=2 C. x1=1,x2=﹣2 D. x1=0,x2=2
查看答案阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
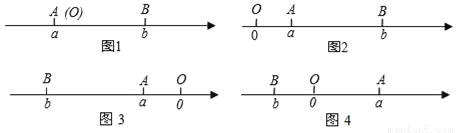
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
查看答案甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.某顾客购买的电器价格是x元.
(1)当x=850时,该顾客应选择在 商场购买比较合算;
(2)当x>1000时,分别用代数式表示在两家商场购买电器所需付的费用;
(3)当x=1700时,该顾客应选择哪一家商场购买比较合算?说明理由.
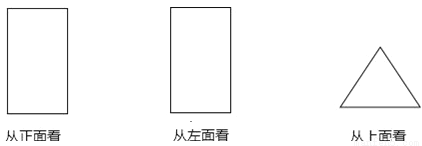
查看答案已知如图为一几何体的三种形状图:
(1)这个几何体的名称为 ;
(2)任意画出它的一种表面展开图;
(3)若从正面看到的是长方形,其长为10cm;从上面看到的是等边三角形,其边长为4cm,求这个几何体的侧面积.
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
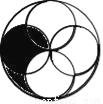
如图,一个大圆和四个面积相等的小圆,已知大圆半径等于小圆直径,小圆半径为a厘米,那么阴影部分的面积为_____平方厘米.
若m是关于x的一元二次方程ax2+bx﹣5=0的一个根,则代数式am2+bm﹣7的值为_____。
查看答案一组数据的方差为S2,将该数据每一个数据,都乘以4,所得到的一组新数据的方差是_________。
查看答案若圆锥的底面半径为3,母线长为6,则圆锥的侧面积等于_____.
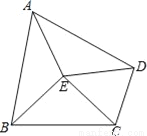
查看答案已知四边形ABCD内有一点E,满足EA=EB=EC=ED,且∠BCD=130°,那么∠BAD的度数为_____.
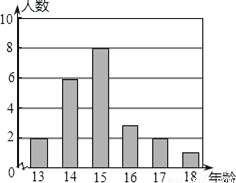
某校男子足球队队员的年龄分布为如图的条形图,则这些队员年龄的众数、中位数分别是_____。
- 题型:填空题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如果规定符号“*”的意义是:a*b= ,试求2*(﹣4)的值.
,试求2*(﹣4)的值.
计算题
(1)﹣8﹣6+22﹣9.
(2)(﹣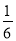 +
+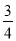 ﹣
﹣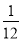 )×48.
)×48.
(3)|﹣0.75|+(﹣3)﹣(﹣0.25)+|﹣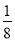 |+
|+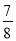 .
.
(4)﹣22+3×(﹣1)4﹣(﹣4)×5.
(5)(7m2n﹣5mn)﹣(4m2n﹣5mn)
(6)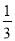 (9a﹣3)+2(a+1).
(9a﹣3)+2(a+1).
若|a|=3,|b|=2,且a>b,则a+b的值可能是:_____.
查看答案数轴上到点﹣3的距离是3个单位长度的点表示的数是_____.
查看答案已知单项式3amb2与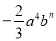 的和是单项式,那么m=_____,n=_____.
的和是单项式,那么m=_____,n=_____.
某种零件,标明要求是φ20±0.02 mm(φ表示直径,单位:毫米),经检查,一个零件的直径是19.9 mm,该零件________ (填“合格”或“不合格”).
查看答案 试题属性- 题型:解答题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若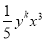 与
与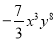 是同类项,则k=_____.
是同类项,则k=_____.
单项式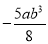 的系数是 ,次数是 .
的系数是 ,次数是 .
“早穿皮袄午穿纱”这句民谣形象地描绘了我们新疆奇妙的气温变化现象.乌鲁木齐市五月的某一天,最低气温是t ℃,温差是15 ℃,则当天的最高气温是________℃.
查看答案某种品牌的彩电降价30%以后,每台售价为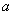 元,则该品牌彩电每台原价应为( )
元,则该品牌彩电每台原价应为( )
A. 0.7a元 B. 0.3a元 C. 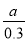 元 D.
元 D. 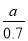 元
元
用四舍五入法按要求对0.05019分别取近似值,其中错误的是( )
A. 0.1(精确到0.1) B. 0.05(精确到千分位)
C. 0.05(精确到百分位) D. 0.0502(精确到0.0001)
查看答案下列各式计算中,正确的是( )
A. 2a+2=4a B. ﹣2x2+4x2=2x2 C. x+x=x2 D. 2a+3b=5ab
查看答案 试题属性- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若规定收入为“+”,那么﹣50元表示( )
A.收入了50元
B.支出了50元
C.没有收入也没有支出
D.收入了100元
B 【解析】 试题分析:若规定收入为“+”,则“﹣”表示与之相反的意义,即支出. 【解析】 ∵收入用“+”表示,∴﹣50元表示支出50元,故选B.(1)阅读理【解析】
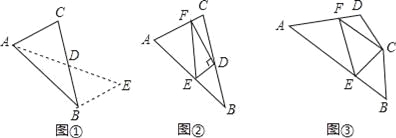
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
下面是某同学对多项式(x2﹣4x﹣3)(x2﹣4x+1)+4进行因式分解的过程.
【解析】
设x2﹣4x=y
原式=(y﹣3)(y+1)+4(第一步)
=y2﹣2y+1 (第二步)
=(y﹣1)2 (第三步)
=(x2﹣4x﹣1)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的 .
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)请你模仿以上方法尝试对多项式(x2+2x)(x2+2x+2)+1进行因式分解.
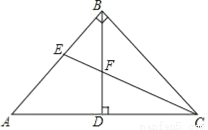
查看答案如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.
(1)求证:△BEF是等腰三角形;
(2)求证:BD=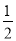 (BC+BF).
(BC+BF).
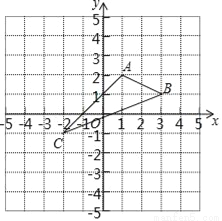
在平面直角坐标系中,A(1,2)、B(3,1)、C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出△ABC关于x轴对称△A2B2C2的各项点坐标A2 ,B2 ,C2 ;
(3)求△ABC的面积.
(1)已知x+y=15,x2+y2=113,求x2﹣3xy+y2的值;
(2)先化简,再求值:(2x﹣1)2﹣(3x+1)(3x﹣1)+5x(x﹣1),x=﹣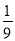 .
.
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
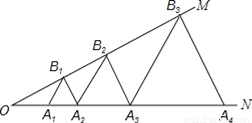
如图,已知∠MON=30°,点A1、A2、A3,…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4 …均为等边三角形,若OA1=1,则△A2016B2016A2017的边长为_____.
已知a2﹣a﹣1=0,则a2﹣a+2017=_____.
查看答案等腰三角形的周长是25cm,一腰上的中线将周长分为1:2两部分,则此三角形的底边长为_____.
查看答案在平面直角坐标系xOy中,已知点A(2,﹣2),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的有( )个.
A. 5 B. 4 C. 3 D. 2
查看答案若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式.下列三个代数式:①(a﹣b)2;②ab+bc+ca;③a2b+b2c+c2a.其中是完全对称式的是( )
A. ①②③ B. ①③ C. ②③ D. ①②
查看答案如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下三个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°.
其中结论正确的个数是( )
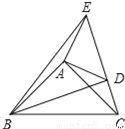
A. 1 B. 2 C. 3 D. 0
查看答案 试题属性- 题型:填空题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
出租车司机老李某天上午营运全是在东西走向的胜利路上进行,如果规定向东为正,向西为负,他这天上午行车里程(单位:公里 )如下:
+8,+4,﹣10,﹣8,+6,﹣2,﹣5,﹣7,+4,+6,﹣8,﹣9
(1)将第几名乘客送到目的地时,老王刚好回到上午出发点?
(2)将最后一名乘客送 到目的地时,老王距上午出发点多远?
(3)若汽车耗油量为0.4升/公里,这天上午老王耗油多少升?
(1)5;(2)21;(3)30.8. 【解析】试题分析:(1)根据题意求和即可; (2)根据题意求和即可; (3)求出所有路程的绝对值的和,再乘以每公里耗油量即可. 试题解析:(1)∵+8+4-10-8+6=0 ∴将第五名乘客送到目的地时,老王刚好回到上午出发点. (2)将最后一名乘客送到目的地时,老王距上午出发点的距离为:+8+4-10-8+6-2-5-7+...先化简,再求值.
(1)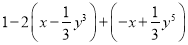 ,其中x=﹣
,其中x=﹣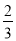 ,y=﹣1.
,y=﹣1.
(2)﹣a2b+(3ab2﹣a2b)﹣2(2ab2﹣a2b),其中a=1,b=﹣2.
查看答案若有理数m、n在数轴上的位置如图所示,请化简:|m+n|+|m﹣n|﹣|n|.
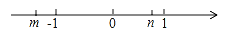
在数轴上有三个点A,B,C,分别表示﹣3,0,2.按下列要求回答:
(1)点A向右移动6个单位后,三个点表示的数谁最大?
(2)点C向左移动3个单位后,这时点B表示的数比点C表示的数大多少?
(3)怎样移动点A,B,C中的两个点,才能使三个点所表示的数相同?有几种办法?分别写出来.
查看答案计算
(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣9);
(2)﹣0.5﹣(﹣3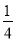 )+2.75﹣7
)+2.75﹣7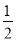 ;
;
(3)(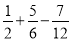 )×(﹣36);
)×(﹣36);
(4)﹣14﹣(5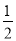 )×
)×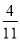 +(﹣2)3+|32+1|
+(﹣2)3+|32+1|
把下列各数填入相应的大括号内:
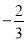 ,
, 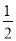 ,﹣0.01,
,﹣0.01, 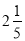 ,7,1,﹣(﹣4),+(﹣1)
,7,1,﹣(﹣4),+(﹣1)
正数集合{ …}
负数集合{ …}
非负整数集合{ …}
分数集合{ …}.
查看答案 试题属性- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
数轴上一点A,一只蚂蚁从A 出发爬了4个单位长度到了原点,则点A所表示的数是( )
A. 4 B. 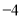 C.
C. 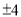 D.
D. 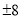
﹣2017的倒数是( )
A. 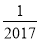 B. ﹣
B. ﹣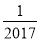 C. 2017 D. ﹣2017
C. 2017 D. ﹣2017
在Rt△ABC中,∠C=90°,BC=6,AC=8,点D在线段AC上从C向A运动.若设CD=x,△ABD的面积为y.
(1)请写出y与x之间的关系式.
(2)当x为何值时,y有最大值,最大值是多少?此时点D在什么位置?
(3)当△ABD的面积是△ABC的面积的一半时,点D在什么位置?
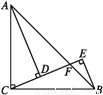
查看答案如图,在△ABC中,∠ACB=90°,AC=BC,CE⊥BE于点E,CE与AB交于点F,AD⊥CF于点D,且AD平分∠FAC.请写出图中两对全等三角形,并选择其中一对加以说明.
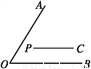
如图,已知∠AOB=α,且PC∥OB,现以P为顶点,PC为一边作∠CPD=α,并用移动三角尺的方法验证,PD与OA是否平行.
某商场为了吸引更多的顾客,安排了一个抽奖活动,并规定:顾客每购买100元商品,就能获得一次抽奖的机会.抽奖规则如下:在抽奖箱内,有100个牌子,分别写有1,2,3,…,100共100个数字,抽到末位数是5的可获20元购物券,抽到数字是88的可获200元购物券,抽到66或99的可获100元购物券.某顾客购物用了130元,他获得购物券的概率是多少?他获得20元、100元、200元购物券的概率分别是多少?
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

