题目内容
17.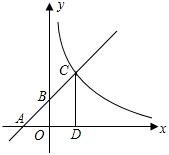 如图,已知一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反此列函数y=$\frac{m}{x}$在第一象限的图象交于点C,CD垂直于x轴,垂足为D.如果OA=OB=OD=1,求:
如图,已知一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反此列函数y=$\frac{m}{x}$在第一象限的图象交于点C,CD垂直于x轴,垂足为D.如果OA=OB=OD=1,求:(1)点C的坐标;
(2)这个一次函数和这个反比例函数的表达式.
分析 (1)根据OA=OB=OD=1得出A、B的坐标,利用待定系数法即可求出一次函数解析式,然后求出点C的坐标;
(2)把C的坐标代入反比例函数的解析式即可得到结论.
解答 解:(1)∵OA=OB=1,
∴A(-1,0),B(0,1),
将A与B代入y=k1x+b得:$\left\{\begin{array}{l}{-{k}_{1}+b=0}\\{b=1}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
则一次函数解析式为y=x+1;
∵OD=2,
∴D(2,0),
∵点C在一次函数y=x+1上,且CD⊥x轴,
∴将x=1代入一次函数解析式得:y=1+1=2,即点C坐标为(1,2);
(2)由(1)求得一次函数解析式为y=x+1,
∵点C在反比例图象上,
∴将C(1,2)代入反比例解析式得:k2=2,
∴反比例函数的表达式为:y=$\frac{2}{x}$.
点评 本题考查了一次函数与反比例函数的交点问题,同时考查用待定系数法求函数解析式,熟练掌握待定系数法求函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是一个圆台及其主视图,你能把它的俯视图和左视图补上吗?
如图是一个圆台及其主视图,你能把它的俯视图和左视图补上吗?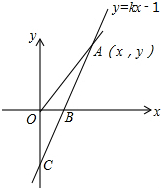 如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且OC=2OB.
如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且OC=2OB. 下面的判断是否正确.说明理由:
下面的判断是否正确.说明理由: