题目内容
在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)若E是线段AC的中点,如图,求证:BE=EF;
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE与EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
 |
证明:(1)∵四边形ABCD为菱形,∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∵E是线段AC的中点,
∴∠CBE=![]() ∠ABC=30°,AE=CE,∵AE=CF,∴CE=CF,∴∠F=∠CEF,
∠ABC=30°,AE=CE,∵AE=CF,∴CE=CF,∴∠F=∠CEF,
∵∠F+∠CEF=∠ACB=60°,∴∠![]() F=30°,∴∠CBE=∠F,∴BE=EF;
F=30°,∴∠CBE=∠F,∴BE=EF;
(2)图2:BE=EF.图3:BE=EF.
图2证明如下:过点E作EG∥BC,交AB于点G,∵四边形ABCD为菱形,∴AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,又∵EG∥BC,∴∠AGE=∠ABC=60°……6分
又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE,…………7分
∴BG=CE,又∵CF=AE,∴GE=CF,…………8分
又∵∠BGE=∠ECF=120°,∴△BGE≌△E![]() CF(SAS),∴BE=EF;……9分.
CF(SAS),∴BE=EF;……9分.
图3证明与图2类似,请酌情赋分。
 |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 14、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数=
14、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数=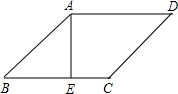 如图,在菱形ABCD中,AE⊥BC于E,已知EC=1,cosB=
如图,在菱形ABCD中,AE⊥BC于E,已知EC=1,cosB= 如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.
如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍. 如图,在菱形ABCD中,P为对角线BD上一点,连接AP,若AP=BP,AD=PD,则∠PAC的度数是( )
如图,在菱形ABCD中,P为对角线BD上一点,连接AP,若AP=BP,AD=PD,则∠PAC的度数是( )