题目内容
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线,交BC于点E.
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由。
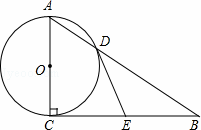
(1)证明:连接CD,
∵AC是直径,
∴∠ADC=90°,
∴∠CDB=90°
∵∠ACB=90°
∴BC是⊙O的切线,
∵DE是⊙O的切线,
 ∴ED=EC
∴ED=EC
∴∠EDC=∠ECD.
又∵∠DCE+∠EBD=∠CDE+∠EDB=90°
∴∠DBE=∠DBE,
∴ED=EB,
∴EB=EC.
(2)解:当以点O、D、E、C为顶点的四边形是正方形时,则∠DEB=90°,
又∵DE=BE,
∴△DEB是等腰直角三角形,则∠B=45°,
∴△ABC是等腰直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 个单位运动时,边EF所在直线和边OC所在直线相交于G,设运动时间为t.
个单位运动时,边EF所在直线和边OC所在直线相交于G,设运动时间为t.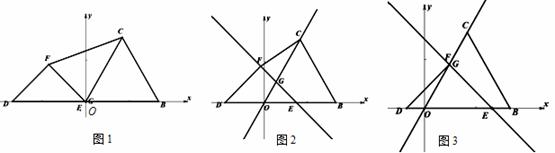
 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.  A.20° B.30°
A.20° B.30°  =
=  B.
B. C.
C. D.
D.


 D.
D.