题目内容
 如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙于E,交AM于D,交BN于C.设AD=x,BC=y.
如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙于E,交AM于D,交BN于C.设AD=x,BC=y.(1)求证:AM∥BN.
(2)探究y与x的函数关系.
考点:切线的性质,切线长定理
专题:
分析:(1)由AM和BN是⊙O的两条切线,可得AB⊥AD,AB⊥BC,则可证得AM∥BN.
(2)首先作DF⊥BN交BC于F,可得四边形ABFD是矩形,然后根据切线长定理得到BF=AD=x,CE=CB=y,则DC=DE+CE=x+y,在直角△DFC中根据勾股定理,就可以求出y与x的关系.
(2)首先作DF⊥BN交BC于F,可得四边形ABFD是矩形,然后根据切线长定理得到BF=AD=x,CE=CB=y,则DC=DE+CE=x+y,在直角△DFC中根据勾股定理,就可以求出y与x的关系.
解答: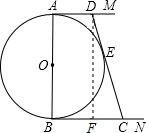 (1)证明:∵AM和BN是⊙O的两条切线,
(1)证明:∵AM和BN是⊙O的两条切线,
∴AB⊥AD,AB⊥BC,
∴AM∥BN.
(2)解:作DF⊥BN交BC于F,
∵AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=2,
∵BC=y,
∴FC=BC-BF=y-x;
∵AM和BN是⊙O的两条切线,DE切⊙O于E,
∴DE=DA=x CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(x-y)2+22,
整理为:y=
,
∴y与x的函数关系为:y=
.
 (1)证明:∵AM和BN是⊙O的两条切线,
(1)证明:∵AM和BN是⊙O的两条切线,∴AB⊥AD,AB⊥BC,
∴AM∥BN.
(2)解:作DF⊥BN交BC于F,
∵AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=2,
∵BC=y,
∴FC=BC-BF=y-x;
∵AM和BN是⊙O的两条切线,DE切⊙O于E,
∴DE=DA=x CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(x-y)2+22,
整理为:y=
| 1 |
| x |
∴y与x的函数关系为:y=
| 1 |
| x |
点评:此题考查了切线的性质、切线长定理、矩形的判定与性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
射击运动员要从甲乙丙丁4名运动员中选拔1名运动员参加比赛,选拔赛中每名队员的平均成绩与方差如表所示,如果要选择一个成绩较高且发挥稳定的人参赛,则选拔的运动员应是( )
| 甲 | 乙 | 丙 | 丁 | |||
| 8 | 9 | 9 | 8 | ||
| S2 | 1 | 1.2 | 1 | 1.3 |
| A、甲 | B、乙 | C、丙 | D、丁 |
下列关于不等式的解的命题中,属于假命题的是( )
| A、不等式x<2有唯一的正整数解 | ||
| B、-2是不等式2x-1<0的一个解 | ||
| C、不等式-3x>9的解集是x>-3 | ||
D、不等式x<
|
 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,BD=4,则BC=
如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,BD=4,则BC=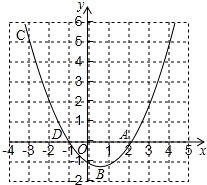 如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(-3,5)三点.
如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(-3,5)三点.