题目内容
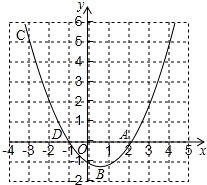 如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(-3,5)三点.
如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(-3,5)三点.(1)求二次函数的关系式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=-x+2,并写出当x在什么范围内时,一次函数的值小于二次函数的值.
考点:抛物线与x轴的交点,待定系数法求二次函数解析式,二次函数与不等式(组)
专题:
分析:(1)把A(2,0),B(0,-1)和C(-3,5)三点代入抛物线解析式y=ax2+bx+c求出a,b,c的值即可;
(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;
(3)画出图象,再根据图象直接得出答案.
(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;
(3)画出图象,再根据图象直接得出答案.
解答:解:(1)把A(2,0),B(0,-1)和C(-3,5)三点代入抛物线解析式y=ax2+bx+c得
,
解得:
.
所以二次函数的解析式为y=
x2-
x-1;
(2)当y=0时,得
x2-
x-1=0;
解得x1=2,x2=-1,
∴点D坐标为(-1,0);
(3)由函数图象可得直线和抛物线的交点为(-3,5)和(2,0),
当一次函数的值小于二次函数的值时,x的取值范围是x>2或x<-3.
|
解得:
|
所以二次函数的解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当y=0时,得
| 1 |
| 2 |
| 1 |
| 2 |
解得x1=2,x2=-1,
∴点D坐标为(-1,0);
(3)由函数图象可得直线和抛物线的交点为(-3,5)和(2,0),
当一次函数的值小于二次函数的值时,x的取值范围是x>2或x<-3.
点评:本题考查了用待定系数法求二次函数的解析式以及一次函数的图象、抛物线与x轴的交点问题,是中档题,要熟练掌握.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
下列判断:①若ab=0,则a=0或b=0或a=0、b=0;②若a2=b2,则a=b;③若ac2=bc2,则a=b;④若|a|>|b|,则(a+b)•(a-b)是正数; ⑤式子
+
(ab≠0)的所有可能的值有4个.其中正确的有( )
| a |
| |a| |
| b |
| |b| |
| A、①④ | B、①②③ | C、①⑤ | D、②③ |
若x=-6是关于x的方程
-(m-x)=1的解,则m的值为( )
| x |
| 3 |
| A、3 | B、9 | C、-9 | D、-3 |
 如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙于E,交AM于D,交BN于C.设AD=x,BC=y.
如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙于E,交AM于D,交BN于C.设AD=x,BC=y.