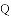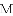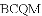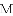题目内容
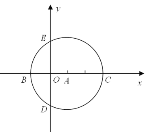
如图,在直角坐标系中,以点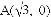 为圆心,以
为圆心,以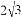 为半径的圆与
为半径的圆与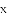
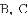
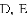
(1)若抛物线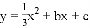 经过
经过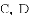
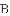
(2)在(1)中的抛物线的对称轴上求一点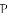
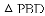
(3)设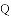
练习册系列答案
相关题目
题目内容
如图,在直角坐标系中,以点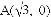 为圆心,以
为圆心,以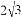 为半径的圆与
为半径的圆与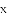
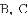
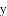
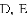
(1)若抛物线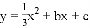 经过
经过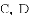
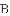
(2)在(1)中的抛物线的对称轴上求一点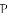
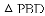
(3)设