题目内容
10.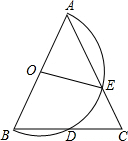 如图,以△ABC一边AB为直径作半圆,与另外两边分别交于点D、E,且点D为BC的中点.
如图,以△ABC一边AB为直径作半圆,与另外两边分别交于点D、E,且点D为BC的中点.(1)证明:△ABC为等腰三角形;
(2)小丽在观察了本题的条件后说:“如果∠B满足一个条件,四边形BDEO就会成为菱形”,你认为小丽的说法正确吗?如果正确,请给出∠B的一个条件,并证明四边形BDEO为菱形;如果不正确,请说明理由.
分析 (1)利用圆周角定理以及线段垂直平分线的性质得出AB=AC得出答案即可;
(2)利用等边三角形的判定方法与性质结合菱形的判定方法得出即可.
解答 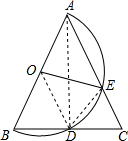 (1)证明:连接AD,
(1)证明:连接AD,
∵AB是半圆直径,
∴∠BDA=90°,
又∵BD=DC,
∴AB=AC,
∴△ABC为等腰三角形;
(2)解:当∠B=60°时,四边形BDEO就会成为菱形,
理由:连接DO,DE,
∵∠B=60°,
∴△ABC是等边三角形,△OBD是等边三角形,
∴△AOE也是等边三角形,△DOE是等边三角形,
∴OB=BD=DE=EO,
∴四边形BDEO是菱形.
点评 此题主要考查了菱形的判定以及等边三角形的判定与性质以及圆周角定理等知识,正确掌握等边三角形的判断与性质是解题关键.

练习册系列答案
相关题目
18.已知圆锥的侧面积是20πcm2,母线长为5cm,则圆锥的底面半径为( )
| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
5.据统计,2014年河南省机动车保有量突破280万辆,对数据“280万”的理解错误的是( )
| A. | 精确到万位 | B. | 有三个有效数字 | ||
| C. | 这是一个精确数 | D. | 用科学记数法表示为2.80×106 |
15. 如图三视图所表示的几何体是( )
如图三视图所表示的几何体是( )
 如图三视图所表示的几何体是( )
如图三视图所表示的几何体是( )| A. | 直三棱柱 | B. | 直四棱柱 | C. | 圆锥 | D. | 不存在 |
20.下列各数中,无理数是( )
| A. | $\frac{22}{7}$ | B. | $\sqrt{9}$ | C. | π | D. | $\root{3}{8}$ |
 如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.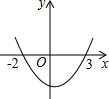 如图,抛物线y=ax2+bx+c交x轴于点A(-2,0)、B(3,0),则不等式ax2+bx+c>0的解集是x>3或x<-2.
如图,抛物线y=ax2+bx+c交x轴于点A(-2,0)、B(3,0),则不等式ax2+bx+c>0的解集是x>3或x<-2.