Question

18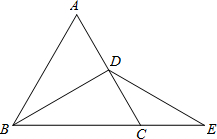．如图，在等腰三角形△ABC中，AB=AC，BD平分∠ABC，在BC的延长线上取一点E，使CE=CD，连接DE，求证：BD=DE．

Answer 1

分析 求出∠ABC=∠ACB，求出∠DBC=$\frac{1}{2}$∠ABC，根据等腰三角形性质和三角形外角性质求出∠E=$\frac{1}{2}$∠ACB，推出∠E=∠DBC即可．

解答 证明：∵AB=AC
∴∠ABC=∠ACB，
∵BD平分∠ABC，
∴∠DBC=$\frac{1}{2}$∠ABC，
∵CD=CE，
∴∠E=∠CDE，
∵∠ACB=∠E+∠CDE，
∴∠E=$\frac{1}{2}$∠ACB，
∴∠E=∠DBE，
∴BD=DE．

点评 本题考查了三角形内角和定理，三角形外角性质和等腰三角形的性质和判定的应用，主要考查学生的推理能力和计算能力．