题目内容
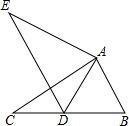 如图,在△ABC中,AB=3,BC=5,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为
如图,在△ABC中,AB=3,BC=5,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为考点:旋转的性质
专题:计算题
分析:根据旋转的性质得AD=AB,由∠B=60°,于是可判断△ADB为等边三角形,根据等边三角形的性质得BD=AB=3,然后利用CD=BC-BD进行计算.
解答:解:∵△ABC绕点A按顺时针旋转一定角度得到△ADE,点B的对应点D恰好落在BC边上,
∴AD=AB,
∵∠B=60°,
∴△ADB为等边三角形,
∴BD=AB=3,
∴CD=BC-BD=5-3=2.
故答案为2.
∴AD=AB,
∵∠B=60°,
∴△ADB为等边三角形,
∴BD=AB=3,
∴CD=BC-BD=5-3=2.
故答案为2.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
若分式方程
=2+
的解为正数,则a的取值范围是( )
| x |
| x-2 |
| a |
| x-2 |
| A、a>4 |
| B、a<4 |
| C、a<4且a≠2 |
| D、a<2且a≠0 |
代数式的家中来了几位客人:
、
、
、
、
,其中属于分式家族成员的有( )
| 2 |
| x |
| x+y |
| 5 |
| 1 |
| 2-a |
| x |
| π-1 |
| x |
| 2x+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |