题目内容
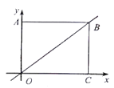
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() (2,2),
(2,2),![]() (-1,2),函数
(-1,2),函数![]() .
.
(1)当函数![]() 的图象经过点
的图象经过点![]() 时,求
时,求![]() 的值并画出直线
的值并画出直线![]() .
.
(2)若![]() ,
,![]() 两点中恰有一个点的坐标(
两点中恰有一个点的坐标(![]() ,
,![]() )满足不等式组
)满足不等式组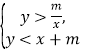 (
(![]() >0),求
>0),求![]() 的取值范围.
的取值范围.
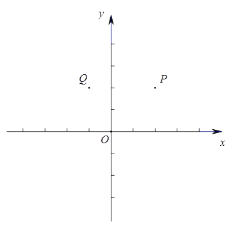
【答案】(1)![]() ,图象详见解析;(2)
,图象详见解析;(2)![]() 的取值范围是:
的取值范围是:![]() ,或
,或![]() .
.
【解析】
(1)把点P的坐标代入函数![]() 即可求出
即可求出![]() 的值,根据一次函数的画法画出直线
的值,根据一次函数的画法画出直线![]() 即可.
即可.
(2)将点P,Q的坐标代入不等式组 分别求出
分别求出![]() 的取值范围,根据
的取值范围,根据![]() ,
,![]() 两点中恰有一个点的坐标满足不等式组,即可求解.
两点中恰有一个点的坐标满足不等式组,即可求解.
解:(1)∵函数![]() 的图象经过点
的图象经过点![]() ,
,
∴![]() ,即
,即![]() .
.
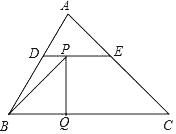
图象如图所示.

(2)当点![]() 满足
满足 (
(![]() >0)时,
>0)时,
解不等式组 得
得![]() .
.
当点![]() 满足
满足 (
(![]() >0)时,
>0)时,
解不等式组![]() 得
得![]() .
.
∵![]() 两点中恰有一个点的坐标满足
两点中恰有一个点的坐标满足 (
(![]() >0),
>0),
∴![]() 的取值范围是:
的取值范围是:![]() ,或
,或![]() .
.

练习册系列答案
相关题目
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?