Question

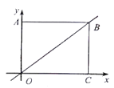
【题目】如图,在直角坐标系中,矩形的顶点与坐标原点重合,顶点分别在坐标轴的正半轴上, ,点在直线上,直线与折线有公共点.

（1）点的坐标是 ；

（2）若直线经过点，求直线的解析式；

（3）对于一次函数，当随的增大而减小时，直接写出的取值范围.

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）OA=6，即BC=6，代入，即可得出点B的坐标

（2）将点B的坐标代入直线l中求出k即可得出解析式

（3）一次函数，必经过，要使y随x的增大而减小，即y值为，分别代入即可求出k的值.

解：∵OA=6，矩形OABC中，BC=OA

∴BC=6

∵点B在直线上，

，解得x=8

故点B的坐标为（8，6）

故答案为（8，6）

（2）把点的坐标代入得，

解得：

∴

（3））∵一次函数，必经过），要使y随x的增大而减小

∴y值为

∴代入，

解得.