Question

如图，AB是⊙O的直径，把AB分成几条相等的线段，以每条线段为直径分别画小圆，设AB=a，那么⊙O的周长L=πa．
（1）计算：①把AB分成两条相等的线段，每个小圆的周长

 

；
②把AB分成三条相等的线段，每个小圆的周长L₃=

 

；
③把AB分成四条相等的线段，每个小圆的周长L₄=

 

；
…
④把AB分成n条相等的线段，每个小圆的周长L_n=

 

；
（2）请仿照上面的探索方法和步骤，计算并导出：当把大圆直径平均分成n等分时，以每条线段为直径画小圆，那么每个小圆的面积S_n与大圆的面积S的关系是：S_n=

 

S．

Answer 1

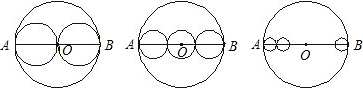
分析：根据圆的面积公式，将每个圆的面积计算出来，找到和周长L的关系即可．

解答：解：（1）根据L=πd，
①把AB分成两条相等的线段，每个小圆的周长L₂=

1

2

πa=

1

2

L；
②把AB分成三条相等的线段，每个小圆的周长L₃=

1

3

πa=

1

3

L，
③把AB分成四条相等的线段，每个小圆的周长L₄=

1

4

πa=

1

4

L；
④把AB分成n条相等的线段，每个小圆的周长L_n=

1

n

πa=

1

n

L．

（2）以a为直径的圆的面积为S₁=π(

a

2

)2=π

a2

4

．
把AB分成两条相等的线段，每个小圆的面积S₂=π(

a

4

)2=

1

4

π(

a

2

)2=

1

22

S₁；
把AB分成三条相等的线段，每个小圆的面积S₃=π(

a

6

)2=

1

9

π(

a

2

)2=

1

32

S₁；
把AB分成四条相等的线段，每个小圆的面积S₄=π(

a

8

)2=

1

16

π(

a

2

)2=

1

42

S₁；
把AB分成n条相等的线段，每个小圆的面积S_n=

1

n2

S₁．

点评：此题是一道规律探索题，需要先进行计算，将每个特殊的圆的面积计算出来，通过总结规律得出一般公式．