��Ŀ����
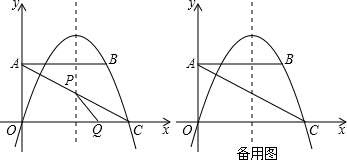
��֪����ֱ������COAB�У�OC��AB����OΪԭ�㽨��ƽ��ֱ������ϵ��A��B��C���������ֱ�ΪA��8��0����B��8��10����C��0��4������DΪ�߶�BC���е㣬����P�ӵ�O��������ÿ��1����λ���ٶȣ�������OABD��·���ƶ����ƶ���ʱ��Ϊt�룮
��1����ֱ��BC�Ľ���ʽ��
��2��������P���߶�OA���ƶ�����tΪ��ֵʱ���ı���OPDC�����������COAB����ģ�
��3������P�ӵ�O������������OABD��·���ƶ������У����OPD�����ΪS����д��S��t�ĺ�����ϵʽ����ָ���Ա���t��ȡֵ��Χ��
��1����ֱ��BC�Ľ���ʽ��
��2��������P���߶�OA���ƶ�����tΪ��ֵʱ���ı���OPDC�����������COAB����ģ�
��3������P�ӵ�O������������OABD��·���ƶ������У����OPD�����ΪS����д��S��t�ĺ�����ϵʽ����ָ���Ա���t��ȡֵ��Χ��

��𣺽⣺��1����ֱ��BC�Ľ���ʽΪy=kx+b��ֱ�߹�B��8��10����C��0��4����
�� ��
��
��� ��
��
����ʽΪy= x+4��
x+4��
��2���ߵ�DΪ�߶�BC���е㣬
��D��4��7��
�������7t��
 =
=
���t= ��s����
��s����
��3����P��OA��ʱ��S= ��t��7=
��t��7= t ��0��t��8��
t ��0��t��8��
��P��AB��ʱ��S= ��4+10����8��
��4+10����8�� ��4��4��
��4��4�� ��8����t��8��
��8����t��8�� ��
��
S=��2t+44��8��t��18��
��P��BD��ʱ��S=S����OCAB��S������OCD��S������OPA��S������ABP
=56��8��4[10�� ��t��18��]��5��t��18��
��t��18��]��5��t��18��
=�� t+
t+ ����18��t��23��
����18��t��23��
��P��OD��ʱ��S=0��23��t��23+ �����������⣬��ȥ����
�����������⣬��ȥ����
��1������ʽΪy= t+4��
t+4��
��2����t= ��s��ʱ���ı���OPDC�����������COAB�����
��s��ʱ���ı���OPDC�����������COAB����� ��
��
��3���ֱ���S= ��t��7=
��t��7= t��0��t��8����
t��0��t��8����
S=��2t+44��8��t��18����
S= =��
=�� t+
t+ ��18��t��23����
��18��t��23����
S=0��23��t��23+ ��������������ȥ����
��������������ȥ����
��
 ��
�� ���
 ��
������ʽΪy=
 x+4��
x+4����2���ߵ�DΪ�߶�BC���е㣬
��D��4��7��
�������7t��

 =
=
���t=
 ��s����
��s������3����P��OA��ʱ��S=
 ��t��7=
��t��7= t ��0��t��8��
t ��0��t��8�� ��P��AB��ʱ��S=
 ��4+10����8��
��4+10����8�� ��4��4��
��4��4�� ��8����t��8��
��8����t��8�� ��
��S=��2t+44��8��t��18��
��P��BD��ʱ��S=S����OCAB��S������OCD��S������OPA��S������ABP
=56��8��4[10��
 ��t��18��]��5��t��18��
��t��18��]��5��t��18��
=��
 t+
t+ ����18��t��23��
����18��t��23�� ��P��OD��ʱ��S=0��23��t��23+
 �����������⣬��ȥ����
�����������⣬��ȥ������1������ʽΪy=
 t+4��
t+4�� ��2����t=
 ��s��ʱ���ı���OPDC�����������COAB�����
��s��ʱ���ı���OPDC�����������COAB����� ��
�� ��3���ֱ���S=
 ��t��7=
��t��7= t��0��t��8����
t��0��t��8����S=��2t+44��8��t��18����
S=
 =��
=�� t+
t+ ��18��t��23����
��18��t��23���� S=0��23��t��23+
 ��������������ȥ����
��������������ȥ����
��ϰ��ϵ�д�
 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ������ϵ�ڣ�����һ��ֱ������AOCD����֪AD=3��AO=8��CO=5������P�������ڣ���S��PAD=S��POC��S��PAO=S��PCD����ô��P��������
��ͼ����ƽ��ֱ������ϵ�ڣ�����һ��ֱ������AOCD����֪AD=3��AO=8��CO=5������P�������ڣ���S��PAD=S��POC��S��PAO=S��PCD����ô��P��������
 �����յ�ʱ���������㶼ֹͣ�˶���
�����յ�ʱ���������㶼ֹͣ�˶���