题目内容
如图，AB是半圆的直径，点C、D是半圆上两点，∠ABC=50°，则∠ADC=考点：圆内接四边形的性质
专题：
分析：由AB是半圆的直径，点C、D是半圆上两点，∠ABC=50°，根据圆的内接四边形的对角互补的性质求解即可求得答案．
解答：解：∵AB是半圆的直径，点C、D是半圆上两点，∠ABC=50°，
∴∠ADC=180°-∠ABC=130°．
故答案为：130°．
∴∠ADC=180°-∠ABC=130°．
故答案为：130°．
点评：此题考查了圆的内接四边形的性质．此题比较简单，注意熟记定理是解此题的关键．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
下面几何体的三种视图有无错误？如果有，请改正．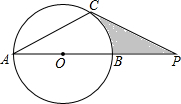
如图，已知：⊙O的直径AB与弦AC的夹角∠A=30°，AC=CP．
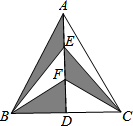如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积28cm2，则图中阴影部分的面积是等腰三角形的一个内角为50°，则这个三角形的底角为（ ）
| A、50°、50° |
| B、80°、80° |
| C、65°、65°或50° |
| D、65°、65° |
画出下列三棱柱的三视图．