题目内容
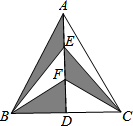 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积28cm2,则图中阴影部分的面积是
如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积28cm2,则图中阴影部分的面积是考点:轴对称的性质
专题:
分析:根据等腰三角形的性质可得BD=CD,再根据轴对称性判断出阴影部分的面积等于△ABC的面积的一半,然后计算即可得解.
解答:解:∵AB=AC,AD是BC边上的高,
∴BD=CD,
∵点E、F是AD的三等分点,
∴阴影部分的面积等于△ABC的面积的一半,
∵△ABC的面积28cm2,
∴阴影部分的面积=14cm2.
故答案为:14.
∴BD=CD,
∵点E、F是AD的三等分点,
∴阴影部分的面积等于△ABC的面积的一半,
∵△ABC的面积28cm2,
∴阴影部分的面积=14cm2.
故答案为:14.
点评:本题考查了轴对称的性质,等腰三角形三线合一的性质,熟记性质并判断出阴影部分的面积等于△ABC的面积的一半是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
下列语句中,正确的是( )
| A、xy+1是一个一次二项式 | ||||
B、-
| ||||
| C、x2y和-yx2是同类项 | ||||
| D、-a3b2c的次数是5 |
若将方程x2-6x+5=0配方成(x+m)2=n的形式,则m、n的值为( )
| A、m=-3,n=4 |
| B、m=3,n=4 |
| C、m=-3,n=-4 |
| D、m=3,n=-4 |
 如图,AB是半圆的直径,点C、D是半圆上两点,∠ABC=50°,则∠ADC=
如图,AB是半圆的直径,点C、D是半圆上两点,∠ABC=50°,则∠ADC= 画出如图所示三棱柱的三视图.
画出如图所示三棱柱的三视图.