题目内容
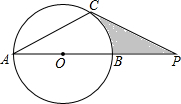 如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.(1)求证:CP是⊙O的切线;
(2)若PC=6,AB=4,求图中阴影部分的面积.
考点:切线的判定,扇形面积的计算
专题:计算题
分析:(1)连结OC,如图,由∠A=30°,AC=CP得到∠P=∠A=30°,加上∠OCA=∠A=30°,则根据三角形外角性质得∠POC=∠A+∠OCA=60°,根据三角形内角和定理可计算出∠PCO=90°,则OC⊥PC,然后根据切线的判定定理得到PC是⊙O的切线;
(2)利用S影阴部分=S△POC-S扇形BOC和扇形的面积公式计算.
(2)利用S影阴部分=S△POC-S扇形BOC和扇形的面积公式计算.
解答:解: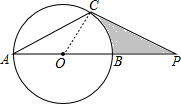 (1)连结OC,如图,
(1)连结OC,如图,
∵∠A=30°,AC=CP,
∴∠P=∠A=30°,
∵OC=OA,
∴∠OCA=∠A=30°,
∴∠POC=∠A+∠OCA=60°,
∴∠PCO=180°-∠P-∠POC=90°
∴OC⊥PC,
∴PC是⊙O的切线;
(2)∵AB=4,
∴OC=2,
∴S影阴部分=S△POC-S扇形BOC
=
•2•6-
=6-
π.
 (1)连结OC,如图,
(1)连结OC,如图,∵∠A=30°,AC=CP,
∴∠P=∠A=30°,
∵OC=OA,
∴∠OCA=∠A=30°,
∴∠POC=∠A+∠OCA=60°,
∴∠PCO=180°-∠P-∠POC=90°
∴OC⊥PC,
∴PC是⊙O的切线;
(2)∵AB=4,
∴OC=2,
∴S影阴部分=S△POC-S扇形BOC
=
| 1 |
| 2 |
| 60•π•22 |
| 360 |
=6-
| 2 |
| 3 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了扇形面积的计算.

练习册系列答案
相关题目
 有理数,a在b数轴上的位置如图所示,则下列各式正确的是( )
有理数,a在b数轴上的位置如图所示,则下列各式正确的是( )| A、a+b>0 | B、|a|>b |
| C、ab>0 | D、a-b>0 |
若将方程x2-6x+5=0配方成(x+m)2=n的形式,则m、n的值为( )
| A、m=-3,n=4 |
| B、m=3,n=4 |
| C、m=-3,n=-4 |
| D、m=3,n=-4 |
 如图,AB是半圆的直径,点C、D是半圆上两点,∠ABC=50°,则∠ADC=
如图,AB是半圆的直径,点C、D是半圆上两点,∠ABC=50°,则∠ADC=