Question

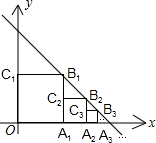（2013•建宁县质检）正方形OA₁B₁C₁、A₁A₂B₂C₂、A₂A₃B₃C₃┅按如图放置，其中点A₁、A₂、A₃┅在x轴的正半轴上，点B₁、B₂、B₃┅在直线y=-x+2上，依此类推┅，则点A_n的坐标为

（

2n-1

2n-1

，0）或（2-

1

2n-1

，0）或（1+

1

2

+

1

4

…

1

2n-1

，0）

．

Answer 1

分析：首先根据直线的解析式，分别求得B₁，B₂，B₃…的坐标，可以得到一定的规律，从而求得A₁，A₂，A₃…的坐标，得到规律，据此即可求解．

解答：解：∵四边形OA₁B₁C₁是正方形，∴A₁B₁=B₁C₁．
∵点B₁在直线y=-x+2上，∴设B₁的坐标是（x，-x+2），
∴x=-x+2，x=1．∴B₁的坐标是（1，1）．∴点A₁的坐标为（1，0）．
∵A₁A₂B₂C₂是正方形，∴B₂C₂=A₁C₂，
∵点B₂在直线y=-x+2上，∴B₂C₂=B₁C₂，
∴B₂C₂=

1

2

A₁B₁=

1

2

，
∴OA₂=OA₁+A₁A₂=1+

1

2

，∴点A₂的坐标为（1+

1

2

，0）．
同理，可得到点A₃的坐标为（1+

1

2

+

1

22

，0）．
依此类推，可得到点A_n的坐标为（1+

1

2

+

1

4

…

1

2n-1

，0）．
1+

1

2

+

1

4

…

1

2n-1

=

2n-1

2n-1

=2-

1

2n-1

．
故答案为（

2n-1

2n-1

，0）或（2-

1

2n-1

，0）或（1+

1

2

+

1

4

…

1

2n-1

，0）．

点评：此题主要考查了一次函数的性质和坐标的变化规律，正确得到点的坐标的规律是解题的关键．