题目内容
4. 如图,是某油路管道的一部分,延伸其中三条支路恰好构成一个直角三角形,其三边长分别为6cm,8cm,10cm,输油中心O在到三条支路距离相等的地方,则中心O到三条支路的管道总长(计算时视管道为线,中心O为点)为( )
如图,是某油路管道的一部分,延伸其中三条支路恰好构成一个直角三角形,其三边长分别为6cm,8cm,10cm,输油中心O在到三条支路距离相等的地方,则中心O到三条支路的管道总长(计算时视管道为线,中心O为点)为( )| A. | 24cm | B. | 12cm | C. | 10cm | D. | 6cm |
分析 根据三角形的面积公式,Rt△ABC的面积等于△AOB、△AOC、△BOC三个三角形面积的和列式求出点O到三边的距离,然后乘以3即可.
解答  解:设点O到三边的距离为h,
解:设点O到三边的距离为h,
则S△ABC=$\frac{1}{2}$×8×6=$\frac{1}{2}$×(8+6+10)×h,
解得h=2m,
∴O到三条支路的管道总长为:3×2=6cm.
故选D.
点评 本题考查了角平分线上的点到两边的距离相等的性质,以及勾股定理,三角形的面积的不同表示,根据三角形的面积列式求出点O到三边的距离是解题的关键.

练习册系列答案
相关题目
12.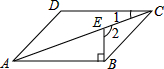 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=18°,则∠2=( )
如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=18°,则∠2=( )
 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=18°,则∠2=( )
如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=18°,则∠2=( )| A. | 98° | B. | 102° | C. | 108° | D. | 118° |
13. 如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )
如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )
 如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )
如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )| A. | 云 | B. | 龙 | C. | 湖 | D. | 丽 |
19.对于计算(a+b)(-a-b),下面的说法正确的是( )
| A. | 能用完全平方公式,结果是-a2-2ab-b2 | |
| B. | 能用完全平方公式,结果是a2-2ab+b2 | |
| C. | 能用完全平方公式,结果是a2+2ab+b2 | |
| D. | 能用平方差公式,结果是a2-b2 |
9.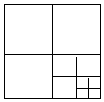 连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
 连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2017}$ | B. | ($\frac{1}{2}$)2017 | C. | ($\frac{1}{4}$)2017 | D. | 1-($\frac{1}{4}$)2017 |
13.某大学生创业团队有研发、管理和探作三个小组,各组的日工资和人数如下表:
现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中正确的有( )个
①团队平均日工资增大;②日工资的方差减小;③曰工资的中位数不变;④日工资的众数不变.
| 研发组 | 管理组 | 操作组 | |
| 日工资(元/人) | 300 | 280 | 260 |
| 人数(人) | 3 | 4 | 5 |
①团队平均日工资增大;②日工资的方差减小;③曰工资的中位数不变;④日工资的众数不变.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.一次函数y=kx+3的图象与坐标轴围成的直角三角形的斜边长是5,且y的值随x值的增大而减小,则k的值为( )
| A. | 4 | B. | -4 | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
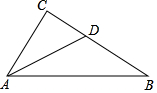 如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BC=16,CD=6,则AC=12.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BC=16,CD=6,则AC=12.