题目内容
20.关于x的方程kx2+3x-1=0有实数根,则k的取值范围是k≥-$\frac{9}{8}$.分析 分类讨论:当k=0,方程变形为3x-1=0,此一元一次方程有解;当k≠0,△=9-4k×(-1)≥0,方程有两个实数解,得到k≥-$\frac{9}{4}$且k≠0,然后综合两种情况即可得到实数k的取值范围
解答 解:当k=0,方程变形为3x-1=0,此一元一次方程的解为x=$\frac{1}{3}$;
当k≠0,△=9-4k×(-1)≥0,解得k≥-$\frac{9}{4}$,即k≥-$\frac{9}{4}$且k≠0时,方程有两个实数根,
综上所述实数k的取值范围为k≥-$\frac{9}{4}$.
故答案为:k≥-$\frac{9}{4}$.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
8.某同学用一扇形纸片为玩偶制作了一个圆锥形帽子(不考虑接缝),已知扇形的半径为13cm,扇形的弧长为10π cm,那么这个圆锥形帽子的高是( )
| A. | 5cm | B. | 12cm | C. | 13cm | D. | 14cm |
10.流花河上周末的水位为73.1米,下表时本周内水位的变化情况:(“+”表示水位比前一天上升,“-”号表示水位比前一天下降)
(1)试一试,根据上表,请你计算哪天水位最高?
(2)本周日的水位是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位变化/米 | +0.30 | +0.25 | -0.55 | +0.40 | +0.20 | -0.55 | +0.05 |
(2)本周日的水位是多少?
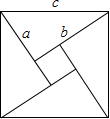 勾股定理是一条古老的数学定理,它神秘而美妙.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.它有很多种证明方法,其技巧各有不同.我国汉代数学家赵爽就根据弦图,利用面积法进行了证明.请你根据右图证明勾股定理.
勾股定理是一条古老的数学定理,它神秘而美妙.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.它有很多种证明方法,其技巧各有不同.我国汉代数学家赵爽就根据弦图,利用面积法进行了证明.请你根据右图证明勾股定理.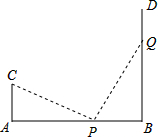 如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动4分钟后△CAP与△PQB全等.
如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动4分钟后△CAP与△PQB全等.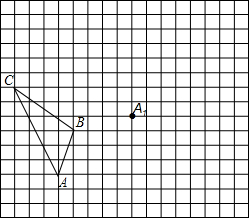 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.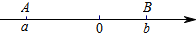 阅读材料:我们知道,若点A、B在数轴上分别表示 有理数a、b(如图所示),A、B两点间的距离表示为AB,则AB=|a-b|.所以式子|x-2|的几何意义是数轴上表示x的点与表示2的点之间的距离.根据上述材料,解答下列问题:
阅读材料:我们知道,若点A、B在数轴上分别表示 有理数a、b(如图所示),A、B两点间的距离表示为AB,则AB=|a-b|.所以式子|x-2|的几何意义是数轴上表示x的点与表示2的点之间的距离.根据上述材料,解答下列问题: