题目内容
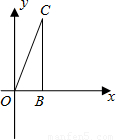
已知:如图,△OBC内接于圆,圆与直角坐标系的x、y轴交于B、A两点,若∠BOC=45° ,∠OBC=75°,A点坐标为(0,2).
,∠OBC=75°,A点坐标为(0,2).求:(1)B点的坐标;
(2)BC的长.
分析:(1)构造以AB为斜边的直角三角形,利用三角形的内角和定理可得∠C的度数,利用同弧所对的圆周角相等可得∠OAB的度数,进而利用∠OAB的正切值可求得OB长,也就求得了点B的坐标;
(2)作出以BC为斜边的直角三角形,利用45°的余弦值可求得BE长,进而利用60°的正弦值可求得BC长.
(2)作出以BC为斜边的直角三角形,利用45°的余弦值可求得BE长,进而利用60°的正弦值可求得BC长.
解答: 解:(1)连接AB(1分)
解:(1)连接AB(1分)
∵∠BOC=45°,∠OBC=75°,
∴∠OAB=∠OCB=60°.(2分)
∵A点坐标为(0,2),
∴AO=2.
在Rt△AOB中,tanBAO=
,
∴OB=AO•tan60°=2
,
∴B点的坐标为(2
,0);(3分)
(2)作BE⊥OC于E(4分).
∵∠BOE=45°,
∴OE=BE.
在Rt△BEO中,OE2+BE2=OB2,BE=
,(5分)
在Rt△BEC中,sin∠C=
,
∴BC=
=
=2
(6分).
 解:(1)连接AB(1分)
解:(1)连接AB(1分)∵∠BOC=45°,∠OBC=75°,
∴∠OAB=∠OCB=60°.(2分)
∵A点坐标为(0,2),
∴AO=2.
在Rt△AOB中,tanBAO=
| OB |
| AO |
∴OB=AO•tan60°=2
| 3 |
∴B点的坐标为(2
| 3 |
(2)作BE⊥OC于E(4分).
∵∠BOE=45°,
∴OE=BE.
在Rt△BEO中,OE2+BE2=OB2,BE=
| 6 |
在Rt△BEC中,sin∠C=
| BE |
| BC |
∴BC=
| BE |
| sin∠C |
| ||||
|
| 2 |
点评:考查锐角三角函数的运用;注意构造所求边所在的有特殊角的直角三角形.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 (2012•鄂州)已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=
(2012•鄂州)已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=

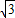 ,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2012C2012,则m= .点C2012的坐标是 .
,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2012C2012,则m= .点C2012的坐标是 .