题目内容
14.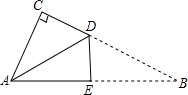 小明拿一张如图的直角三角形纸片ABC,其中∠C=90°,他将纸片沿DE折叠,使点B与点A重合,∠CAD:∠BAD=4:3,则∠CDA的度数为54°.
小明拿一张如图的直角三角形纸片ABC,其中∠C=90°,他将纸片沿DE折叠,使点B与点A重合,∠CAD:∠BAD=4:3,则∠CDA的度数为54°.
分析 设∠CAD=4x,∠BAD=3x,根据翻折的性质可得∠B=∠BAD,然后根据直角三角形两锐角互余列方程求出x,从而得到∠CAD,再根据直角三角形两锐角互余列式计算即可得解.
解答 解:∵∠CAD:∠BAD=4:3,
∴∠CAD=4x,∠BAD=3x,
由翻折的性质得,∠B=∠BAD=3x,
在Rt△ABC中,∠BAC+∠B=90°,
∴4x+3x+3x=90°,
解得x=9°,
∴∠CAD=4×9°=36°,
∴∠CDA=90°-∠CAD=90°-36°=54°.
故答案为:54°.
点评 本题考查了直角三角形两锐角互余的性质,翻折变换的性质,熟记各性质并列出方程是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
19.对15名男生60秒跳绳的成绩进行统计,结果如下表所示:
则这15个数据的极差和众数分别是( )
| 跳绳的成绩(个) | 135 | 140 | 145 | 150 | 155 |
| 人数(人) | 3 | 4 | 5 | 2 | 1 |
| A. | 20,5 | B. | 20,145 | C. | 4,145 | D. | 20,155 |
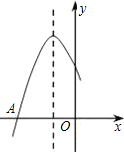 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是①④.
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是①④.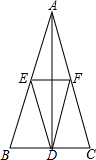 文文画了一个等腰△ABC,如图,AB=AC,他又画出BC边上的高AD,在AB上任取一点E过点E作EF∥BC,交AC于点F,然后他写下两个结论.
文文画了一个等腰△ABC,如图,AB=AC,他又画出BC边上的高AD,在AB上任取一点E过点E作EF∥BC,交AC于点F,然后他写下两个结论.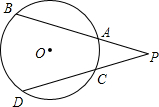 如图,$\widehat{BD}$=100°,$\widehat{AC}$=30°,则∠P=35°.
如图,$\widehat{BD}$=100°,$\widehat{AC}$=30°,则∠P=35°.