题目内容
8.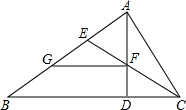 如图,Rt△ABC中,∠BAC=90°,AD是高,CE是角平分线,AE、CE交于点F.
如图,Rt△ABC中,∠BAC=90°,AD是高,CE是角平分线,AE、CE交于点F.(1)判断△AEF的形状,并说明理由;
(2)作FG∥BC交AB于点G,求证:AF=BG.
分析 (1)结论:△AEF是等腰三角形,只要证明∠AEF=∠AFE即可.
(2)作EH⊥BC于H,只要证明△AFG≌△EHB,再利用等量代换即可得到AG=EB.
解答 (1)解:结论:△AEF是等腰三角形.
理由:∵AD为△ABC的高,EC平分∠ACD,
∴∠ADC=90°,∠ACE=∠ECB,
∵∠B+∠ACB=90°,∠DAC+∠ACB=90°,
∴∠B=∠DAC,
∵∠AEC=∠B+∠ECB,
∴∠AEC=∠DAC+∠ECA=∠AFE,
∴AE=AF,
∴△AEF是等腰三角形.
(2)证明:作EH⊥BC于H,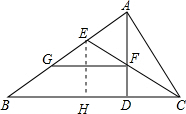 ∵E是角平分线上的点,EH⊥BC,EA⊥CA,
∵E是角平分线上的点,EH⊥BC,EA⊥CA,
∴EA=EH,
∵AE=AF,
∴EH=AF,
∵FG∥BC,
∴∠AGF=∠B,
在△AFG和△EHB中,
$\left\{\begin{array}{l}{∠GAF=∠BEH}\\{∠AGF=∠B}\\{AF=EH}\end{array}\right.$,
∴△AFG≌△EHB(AAS)
∴AG=EB,
即AE+EG=BG+GE,
∴AE=BG.
点评 本题考查了全等三角形的判定与性质、角平分线性质定理等知识,解题的关键是正确寻找全等三角形,出现角平分线应该利用角平分线性质定理添加辅助线,属于中考常考题型.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
3.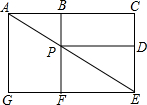 如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )
如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )
 如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )
如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
20.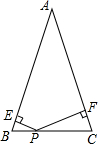 如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )
如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )
 如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )
如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )| A. | 2.5cm | B. | 2$\sqrt{2}$cm | C. | 5cm | D. | 2$\sqrt{3}$cm |
18.下列各曲线中不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |