题目内容
13.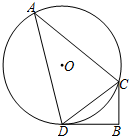 如图,△ACD内接于⊙O,CB垂直于过点D的切线,垂足为B,如果BC=3,sin∠A=$\frac{3}{4}$,那么⊙O的半径为$\frac{8}{3}$.
如图,△ACD内接于⊙O,CB垂直于过点D的切线,垂足为B,如果BC=3,sin∠A=$\frac{3}{4}$,那么⊙O的半径为$\frac{8}{3}$.
分析 作直径DE,连接CE;先由弦切角定理求出∠BDC=∠A,再根据三角函数求出CD,然后在Rt△DCE中,由三角函数求出直径DE,即可得出半径.
解答 解:作直径DE,连接CE,如图所示: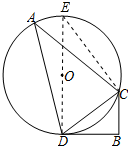 则∠DCE=90°,
则∠DCE=90°,
∵CB垂直于过点D的切线,
∴∠DBC=90°,∠BDC=∠A,
∵BC=3,sin∠A=$\frac{3}{4}$,
∴sin∠BDC=$\frac{BC}{CD}$=$\frac{3}{4}$,
∴CD=4,
∵∠E=∠A,
∴sin∠E=$\frac{CD}{DE}$=$\frac{3}{4}$,
∴DE=$\frac{16}{3}$,
∴OD=$\frac{1}{2}$DE=$\frac{8}{3}$;
故答案为:$\frac{8}{3}$.
点评 本题考查了切线的性质、圆周角定理、弦切角定理以及三角函数的运用;熟练掌握圆的有关定理,通过作辅助线构造直角三角形,正确解直角三角形是解决问题的关键.

练习册系列答案
相关题目
4.已知反比例函数的表达式为$y=\frac{k-1}{x}$,它的图象在各自象限内具有y随x增大而减小的特点,那么k的取值范围是( )
| A. | k>1 | B. | k<1 | C. | k>0 | D. | k<0 |
1. 如图,AB是⊙O的直径,∠BAC=30°,CD⊥AB于点E,BE=2,则⊙O的半径为( )
如图,AB是⊙O的直径,∠BAC=30°,CD⊥AB于点E,BE=2,则⊙O的半径为( )
 如图,AB是⊙O的直径,∠BAC=30°,CD⊥AB于点E,BE=2,则⊙O的半径为( )
如图,AB是⊙O的直径,∠BAC=30°,CD⊥AB于点E,BE=2,则⊙O的半径为( )| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
8.若m与3互为相反数,则|m-3|的值为( )
| A. | 0 | B. | 6 | C. | $\frac{10}{3}$ | D. | $\frac{8}{3}$ |
2.若代数式$\frac{x-2}{x+2}$的值为0,则x等于( )
| A. | 2 | B. | -2 | C. | 0 | D. | 2,-2 |
3.在平面直角坐标系中,点A(-4,-3)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在⊙O中,AB是直径,CD是弦,∠D=40°,则∠AOC=100度.
如图,在⊙O中,AB是直径,CD是弦,∠D=40°,则∠AOC=100度.