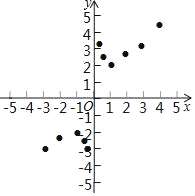题目内容
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据:(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据:
频数 组别 | 165.5~170.5 | 170.5~175.5 | 175.5~180.5 | 180.5~185.5 | 185.5~190.5 | 190.5~195.5 |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 | a | 6 | 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据:
(1)计算甲车间样品的合格率;
(2)估计乙车间生产的8000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
【答案】(1)55%;(2)6000个;(3)乙车间生产的新产品更好,理由见解析.
【解析】
(1)利用所列举的数据得出甲车间样品的合格率;
(2)得出乙车间样品的合格产品数进而得出乙车间样品的合格率进而得出答案;
(3)利用平均数、方差的意义分别分析得出答案.
解:(1)由收集的数据可知,尺寸范围为176mm~185mm的甲车间样品有11个,
∴甲车间样品的合格率为:![]() ×100%=55%.
×100%=55%.
(2)由收集的数据可知,尺寸范围为176mm~185mm的已车间样品有15个,
∴乙车间样品的合格率为:![]() ×100%=75%,
×100%=75%,
∴乙车间的合格产品数为:8000×75%=6000(个),
(3)乙车间生产的新产品更好,理由如下:
①乙车间合格率比甲车间高,所以乙车间生产的新产品更好;
②甲、乙平均数相等,且均在合格范围内,而乙的方差小于甲的方差,说明乙比较稳定.
所以乙车间生产的新产品更好.

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】小明根据学习函数的经验,对函数y=x+![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+![]() 的自变量x的取值范围是_____.
的自变量x的取值范围是_____.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=_____,n=_____;
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | 4 | … |
y | … | ﹣ | ﹣ | ﹣2 | ﹣ | ﹣ | m |
| 2 |
| n |
| … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣![]() 时,x=_____.
时,x=_____.
②写出该函数的一条性质_____.
③若方程x+![]() =t有两个不相等的实数根,则t的取值范围是_____.
=t有两个不相等的实数根,则t的取值范围是_____.