Question

【题目】图1，抛物线与x轴交于A（﹣1，0），B（3，0），顶点为D（1，﹣4），点P为y轴上一动点．

（1）求抛物线的解析式；

（2）在y轴的负半轴上是否存在点P，使△BDP是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．

（3）如图2，点在抛物线上，求的最小值．

Answer 1

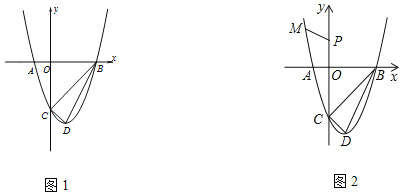
【答案】（1）y＝x2﹣2x﹣3；（2）点P坐标为（0，﹣）或（0，﹣﹣4）或（0，﹣1）;（3）

【解析】

（1）由已知抛物线顶点坐标为D，设抛物线的解析式为y＝a（x﹣1）2﹣4，再把点A代入即可求得二次项系数a的值，由此即可求得抛物线的解析式；（2）由点B、D坐标可求BD的长．设点P坐标为（0，t），用t表示BP2，DP2．对BP＝BD、DP＝BD、BP＝DP三种情况进行分类讨论计算，解方程求得t的值并讨论是否合理即可；（3）由点B、C坐标可得∠BCO＝45°，所以过点P作BC垂线段PQ即构造出等腰直角△PQC，可得PQ＝PC，故有MP+PC＝MP+PQ．过点M作BC的垂线段MH，根据垂线段最短性质，可知当点M、P、Q在同一直线上时，MP+PC＝MP+PQ＝MH最小，即需求MH的长．连接MB、MC构造△BCM，利用y轴分成△BCD与△CDM求面积和即得到△BCM面积，再由S△BCM＝BCMH即求得MH的长．

解：（1）∵抛物线顶点为D（1，﹣4），

∴设抛物线的解析式为y＝a（x﹣1）2﹣4，

∵A（﹣1，0）在抛物线上

∴4a﹣4＝0，解得：a＝1

∴抛物线的解析式为y＝（x﹣1）2﹣4＝x2﹣2x﹣3

（2）在y轴的负半轴上存在点P，使△BDP是等腰三角形．

∵B（3，0），D（1，﹣4）

∴BD2＝（3﹣1）2+（0+4）2＝20

设y轴负半轴的点P坐标为（0，t）（t＜0）

∴BP2＝32+t2，DP2＝12+（t+4）2

①若BP＝BD，则9+t2＝20

解得：t1＝（舍去），t2＝﹣

②若DP＝BD，则1+（t+4）2＝20

解得：t1＝-4（舍去），t2＝﹣﹣4

③若BP＝DP，则9+t2＝1+（t+4）2

解得：t＝﹣1

综上所述，点P坐标为（0，﹣）或（0，﹣﹣4）或（0，﹣1）

（3）连接MC、MB，MB交y轴于点D，过点P作PQ⊥BC于点Q，过点M作MH⊥BC于点H

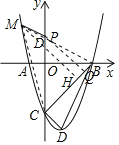
∵x＝0时，y＝x2﹣2x﹣3＝﹣3；

∴C（0，﹣3）；

∵B（3，0），∠BOC＝90°；

∴∠OBC＝∠OCB＝45°，BC＝3

∵∠PQC＝90°

∴Rt△PQC中，sin∠BCO＝＝

∴PQ＝PC,

∴MP+PC＝MP+PQ;

∵MH⊥BC于点H,

∴当点M、P、Q在同一直线上时，MP+PC＝MP+PQ＝MH最小,

∵M（﹣，m）在抛物线上

∴m＝（﹣）2﹣2×（﹣）﹣3＝

∴M（﹣，）

设直线MB解析式为y＝kx+b

∴，

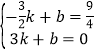解得： ，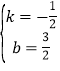

∴直线MB：y＝﹣x+,

∴MB与y轴交点D（0，）,

∴CD＝﹣（﹣3）＝,

∴S△BCM＝S△BCD+S△CDM＝CDBO+CD|xM|＝CD（xB﹣xM）＝××（3+）＝,

∵S△BCM＝BCMH,

∴MH＝=,

∴MP+PC的最小值为.