��Ŀ����
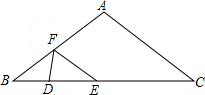 ��ͼ���ڡ�ABC�У�AB=AC=10cm��BC=16cm��DE=4cm���߶�DE���˵�D�ӵ�B��ʼ����BC����1cm/s���ٶ����C�˶������˵�E�����Cʱֹͣ�˶�������E��EF��AC��AB�ڵ�F������DF�����˶���ʱ��Ϊt�루t��0����
��ͼ���ڡ�ABC�У�AB=AC=10cm��BC=16cm��DE=4cm���߶�DE���˵�D�ӵ�B��ʼ����BC����1cm/s���ٶ����C�˶������˵�E�����Cʱֹͣ�˶�������E��EF��AC��AB�ڵ�F������DF�����˶���ʱ��Ϊt�루t��0������1���ú�t�Ĵ���ʽ��ʾ�߶�EF�ij���Ϊ
��2�����˶������У���DEF�ܷ�Ϊ���������Σ����ܣ������t��ֵ�������ܣ���˵�����ɣ�
��3������M���߶�EF���е㣬��ֱ��д���������˶������е�M�˶�·�ߵij���
���㣺�������ۺ���
ר�⣺
��������1����Ϊƽ�У���
=
����BE��AC��BC����֪����EF�ɱ�ʾ��
��2���˶�������ʹ��DEFΪ���������Σ���Ҫ����������Ϊ������Ҫ���������������DF=EFʱ����DE=EFʱ����DE=EFʱ���ֱ������������������ơ��߳ɱ�������1����EF��ֵ�õ�����t�ķ��̣���ü��ɣ�
��3�����˶��켣������Ҫ����M���˶��Ĺ켣������ʲô�������ͼ�ײ��룬�˹켣ΪMN������Ϊ�˶��е�EF����ACƽ�У������ñ߳ɱ����ɵ�AN=CN�����˶�������M�㶼��AC�ߵ������ϣ���Ϊ�����θ�����֪�ҹ̶������ݹ��ɶ��������Ƶ���BN��BM����MN����
| EF |
| AC |
| BE |
| BC |
��2���˶�������ʹ��DEFΪ���������Σ���Ҫ����������Ϊ������Ҫ���������������DF=EFʱ����DE=EFʱ����DE=EFʱ���ֱ������������������ơ��߳ɱ�������1����EF��ֵ�õ�����t�ķ��̣���ü��ɣ�
��3�����˶��켣������Ҫ����M���˶��Ĺ켣������ʲô�������ͼ�ײ��룬�˹켣ΪMN������Ϊ�˶��е�EF����ACƽ�У������ñ߳ɱ����ɵ�AN=CN�����˶�������M�㶼��AC�ߵ������ϣ���Ϊ�����θ�����֪�ҹ̶������ݹ��ɶ��������Ƶ���BN��BM����MN����
����⣺��1���߶�EF�ij���Ϊ
(t+4)cm��
�������£�
��EF��AC��
��
=
��
��AC=10cm��BC=16cm��BE=BD+DE=��t+4��cm��
��EF=
•AC=
•10=
(t+4)cm��
��2���ٵ�DF=EFʱ���С�EDF=��DEF��
��EF��AC��
���DEF=��C��
��AB=AC��
���B=��C��
���B=��C=��DEF=��EDF��
���B���D�غϣ�
��t=0��
�ڵ�DE=DFʱ��
��DE=4cm��EF=
(t+4)cm��
��4=
(t+4)��
��� t=
��
�۵�DE=EFʱ��
BE��BC=EF��AC����BE��16=4��10
���BE=6.4��
t=��6.4-4����1=2.4��
������������t=0��
��ʱ����DEFΪ���������Σ�
��3���߶�EF���е�M�˶�·�ߵij�Ϊ
cm��
�������£�

��ͼ1����t=0��ʱ��B��D�غϣ�����BM���ӳ�����AC��N������A����AP��BC��P������N��NQ��BC��Q��
��EF��AC��
��
=
=
��
��FM=ME��
��AN=NC��
��MN���ǵ�M�˶�·�ߣ�
��Rt��APC��
��PC=
•BC=8cm��AC=10cm��
��AP=6cm��
��NQ��AP��
��CQ=
•PC=4cm��
��Rt��BNQ��
��NQ=
•AP=3cm��BQ=BC-CQ=16-4=12cm��
��BN=3
cm��
��
=
��
��
=
��
��� BM=
cm��
��MN=BN-BM=
cm��
| 5 |
| 8 |
�������£�
��EF��AC��
��
| EF |
| AC |
| BE |
| BC |
��AC=10cm��BC=16cm��BE=BD+DE=��t+4��cm��
��EF=
| BE |
| BC |
| t+4 |
| 16 |
| 5 |
| 8 |
��2���ٵ�DF=EFʱ���С�EDF=��DEF��
��EF��AC��
���DEF=��C��
��AB=AC��
���B=��C��
���B=��C=��DEF=��EDF��
���B���D�غϣ�
��t=0��
�ڵ�DE=DFʱ��
��DE=4cm��EF=
| 5 |
| 8 |
��4=
| 5 |
| 8 |
��� t=
| 12 |
| 5 |
�۵�DE=EFʱ��
BE��BC=EF��AC����BE��16=4��10
���BE=6.4��
t=��6.4-4����1=2.4��
������������t=0��
| 12 |
| 5 |
��3���߶�EF���е�M�˶�·�ߵij�Ϊ
| 9 |
| 4 |
| 17 |
�������£�

��ͼ1����t=0��ʱ��B��D�غϣ�����BM���ӳ�����AC��N������A����AP��BC��P������N��NQ��BC��Q��
��EF��AC��
��
| EM |
| CN |
| BM |
| BN |
| MF |
| NA |
��FM=ME��
��AN=NC��
��MN���ǵ�M�˶�·�ߣ�
��Rt��APC��
��PC=
| 1 |
| 2 |
��AP=6cm��
��NQ��AP��
��CQ=
| 1 |
| 2 |
��Rt��BNQ��
��NQ=
| 1 |
| 2 |
��BN=3
| 17 |
��
| BM |
| BN |
| BE |
| BC |
��
| BM | ||
3
|
| 4 |
| 16 |
��� BM=
| 3 |
| 4 |
| 17 |
��MN=BN-BM=
| 9 |
| 4 |
| 17 |
���������⿼����ƽ���߽صö�Ӧ�߳��ɱ����������������ж������ʣ���λ�����ù��ɶ�������ֱ�������ν�߳��ȳ���֪ʶ�����Ѷ����У���һ���dz�ֵ�ÿ�����ϰ���յ���Ŀ��

��ϰ��ϵ�д�
 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
�����Ŀ