题目内容
 如图,已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,求:∠AFD的度数?
如图,已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,求:∠AFD的度数?考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:根据等边三角形的性质得出AB=BC,∠BAC=∠C=∠ABE=60°,根据SAS推出△ABE≌△BCD,推出∠BAE=∠CBD,根据三角形的外角性质求出∠AFD∠ABC即可.
解答:解:∵△ABC是等边三角形,
∴AB=BC,∠BAC=∠C=∠ABE=60°,
在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠BAE=∠CBD,
∴∠AFD=∠ABF+∠BAE=∠ABF+∠CBD=∠ABC=60°.
∴AB=BC,∠BAC=∠C=∠ABE=60°,
在△ABE和△BCD中,
|
∴△ABE≌△BCD(SAS),
∴∠BAE=∠CBD,
∴∠AFD=∠ABF+∠BAE=∠ABF+∠CBD=∠ABC=60°.
点评:本题考查了全等三角形的性质和判定,三角形的外角性质,等边三角形的性质的应用,解此题的关键是求出△ABE≌△BCD,注意:全等三角形的对应角相等.

练习册系列答案
相关题目
若一个数m用四舍五入法取近似值为2.8,则( )
| A、m=2.80 |
| B、2.75≤m≤2.84 |
| C、2.75<m≤2.84 |
| D、2.75≤m<2.85 |
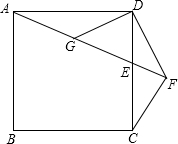 在正方形ABCD中,E为CD上一点,连接AE,过点C作CF⊥AF的延长线于点F,连接DF,过点D作DG⊥DF交AE于点G.
在正方形ABCD中,E为CD上一点,连接AE,过点C作CF⊥AF的延长线于点F,连接DF,过点D作DG⊥DF交AE于点G.
 已知:如图,点A、E、F、C在同一直线上,AD∥BC,AD=CB,AE=CF.求证:∠B=∠D.
已知:如图,点A、E、F、C在同一直线上,AD∥BC,AD=CB,AE=CF.求证:∠B=∠D.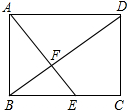 如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.
如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.