Question

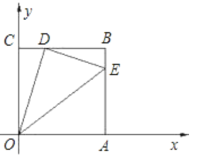
【题目】如图，延长矩形ABCD的边BC至点E，使CE=BD，连结AE，如果∠ABD=60°，那么∠BAE的度数是（　　）

A. 40°B. 55°C. 75°D. 80°

Answer 1

【答案】C

【解析】

连接AC，由矩形性质可得AD∥BE，AC=BD，∠BAD=90°，∠ABD=∠BAC=60°，又可得∠E=∠DAE，可得∠E度数，进而得出∠BAE的度数．

解：连接AC，

∵四边形ABCD是矩形，
∴AD∥BE，AC=BD，∠BAD=90°，∠ABD=∠BAC=60°，
∴∠E=∠DAE，∠CAD=∠BAD-∠BAC=90°-60°=30°，
又∵BD=CE，
∴CE=CA，
∴∠E=∠CAE，
∵∠CAD=∠CAE+∠DAE，
∴∠E+∠E=30°，即∠E=15°．
∴∠BAE=90°-15°=75°，
故选：C．