题目内容
18.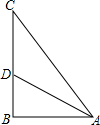 如图,在△ABC中,∠C=90°,AB=6$\sqrt{3}$,∠BAC的平分线AD=12,求∠C的度数.
如图,在△ABC中,∠C=90°,AB=6$\sqrt{3}$,∠BAC的平分线AD=12,求∠C的度数.
分析 根据cos∠BAC=$\frac{AB}{AD}$=$\frac{6\sqrt{3}}{12}$=$\frac{\sqrt{3}}{2}$,于是得到∠BAD=30°,由于∠BAC的平分线是AD,于是得到∠BAC=60°,根据三角形的内角和即可得到结论.
解答 解:∵∠B=90°,
∴cos∠BAD=$\frac{AB}{AD}$=$\frac{6\sqrt{3}}{12}$=$\frac{\sqrt{3}}{2}$,
∴∠BAD=30°,
∵∠BAC的平分线是AD,
∴∠BAC=60°,
∴∠C=30°.
点评 本题考查了解直角三角形,角平分线的定义,熟记解直角三角形的方法是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
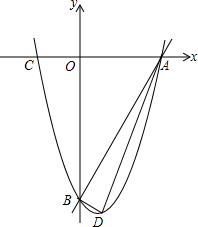 如图,已知一次函数y=2x-8与抛物线y=x2+bx+c都经过x轴上的A点和y轴上的B点.
如图,已知一次函数y=2x-8与抛物线y=x2+bx+c都经过x轴上的A点和y轴上的B点.