题目内容
8.我们知道:1+3+5+7+9+11+…+(2n-1)=n2(n为正整数).(1)试用类比的方法写出1+3+5+7+9+11+…+(4m-3)+(4m-1)(m为正整数)的结果是4m2.
(2)设1+5+9+…+(4m-3)=k,试用含k和m的代数式表示3+7+11+…+(4m-1).
分析 (1)根据已知的式子是连续的奇数的和,结果是数字的个数的平方,据此即可求解;
(2)根据1+3+5+7+9+11+…+(4m-3)+(4m-1)=[1+5+9+…+(4m-3)]+[3+7+11+…+(4m-1)],即可代入求解.
解答 解:(1)1+3+5+7+9+11+…+(4m-3)+(4m-1)
=1+3+5+7+9+11+…+(4m-3)+(2×2m-1)
=(2m)2=4m2.
故答案是:4m2;
(2)∵1+3+5+7+9+11+…+(4m-3)+(4m-1)=[1+5+9+…+(4m-3)]+[3+7+11+…+(4m-1)],
∴k+[3+7+11+…+(4m-1)]=4m2,
∴3+7+11+…+(4m-1)=4m2-k.
点评 本题考查了数字的变化规律,理解1+3+5+7+9+11+…+(4m-3)+(4m-1)=[1+5+9+…+(4m-3)]+[3+7+11+…+(4m-1)]是解决本题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
19.下列计算正确的是( )
| A. | 6x2•3xy=9x3y | B. | (2ab2)•(-3ab)=-a2b3 | C. | (mn)2•(-m2n)=-m3n3 | D. | (-3x2y)(-3xy)=9x3y2 |
17. 一次函数y=kx+b的图象如图所示,则满足y>0的x的取值范围为( )
一次函数y=kx+b的图象如图所示,则满足y>0的x的取值范围为( )
 一次函数y=kx+b的图象如图所示,则满足y>0的x的取值范围为( )
一次函数y=kx+b的图象如图所示,则满足y>0的x的取值范围为( )| A. | x>1 | B. | x>2 | C. | x<1 | D. | x<2 |
 如图,△ABC中,AB=AC,D,E分别是AC、AB上的点,且BD=BC,AD=DE=EB,求∠A的度数.
如图,△ABC中,AB=AC,D,E分别是AC、AB上的点,且BD=BC,AD=DE=EB,求∠A的度数.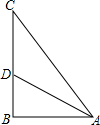 如图,在△ABC中,∠C=90°,AB=6$\sqrt{3}$,∠BAC的平分线AD=12,求∠C的度数.
如图,在△ABC中,∠C=90°,AB=6$\sqrt{3}$,∠BAC的平分线AD=12,求∠C的度数.