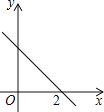题目内容
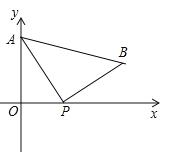
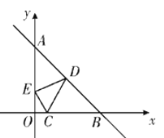
【题目】如图所示,已知点C(1,0),直线![]() 与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
A.![]() B.10
B.10
C.![]() D.12
D.12
【答案】B
【解析】
点C关于OA的对称点C′(-1,0),点C关于直线AB的对称点C″(7,6),连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,可以证明这个最小值就是线段C′C″.
解:如图,点C(1,0)关于y轴的对称点C′(-1,0),点C关于直线AB的对称点C″,

∵直线AB的解析式为y=-x+7,
∴直线CC″的解析式为y=x-1,
由![]()
解得![]() ,
,
∴直线AB与直线CC″的交点坐标为K(4,3),
∵K是CC″中点,C(1,0),
设C″坐标为(m,n),
∴ ,解得:
,解得:![]()
∴C″(7,6).
连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,
△DEC的周长=DE+EC+CD=EC′+ED+DC″=C′C″=![]()
故答案为:10.

练习册系列答案
相关题目