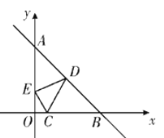
题目内容
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 于
于![]() ,交直线
,交直线![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 在
在![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(3)若![]() 为
为![]() 中点,则当
中点,则当![]() ______度时,四边形
______度时,四边形![]() 是正方形.
是正方形.
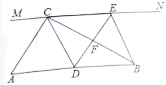
【答案】(1)见解析;(2)四边形![]() 是菱形,理由见解析;(3)
是菱形,理由见解析;(3)![]() 时,四边形
时,四边形![]() 是正方形
是正方形
【解析】
(1)证明四边形![]() 是平行四边形可得结论;
是平行四边形可得结论;
(2)只要证明四边形![]() 是平行四边形及
是平行四边形及![]() ,根据一组邻边相等的平行四边形是菱形可知四边形
,根据一组邻边相等的平行四边形是菱形可知四边形![]() 的形状;
的形状;
(3)由(2)知四边形![]() 是菱形,若四边形
是菱形,若四边形![]() 是正方形,则
是正方形,则![]() ,由题意可知
,由题意可知![]() ,由此可得
,由此可得![]() 的度数.
的度数.
(1)证明:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,即
,即![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ;
;
(2)解:四边形![]() 是菱形,
是菱形,
理由是:∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴四边形![]() 是菱形;
是菱形;
(3)由(2)知四边形![]() 是菱形,若四边形
是菱形,若四边形![]() 是正方形,则
是正方形,则![]()
![]()
又![]() ,
,![]() 为
为![]() 中点
中点
![]()
![]()
故当![]() 时,四边形
时,四边形![]() 是正方形
是正方形

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目