Question

【题目】如图，在RI△ABC中，∠C=90°，AC=BC=4cm，点P从点A出发沿线段AB以cm/s的速度向点B运动，设运动时间为ts．过点P作PD⊥AB，PD与△ABC的腰相交于点D．

（1）当t=（4-2）s时，求证：△BCD≌△BPD；

（2）当t为何值时，S△APD=3S△BPD，请说明理由．

Answer 1

【答案】（1）见解析；（2）当t为3s时，S△APD=3S△BPD．理由见解析.

【解析】

（1）由勾股定理得出AB=AC=4cm，当t=（4-2）s时，AP=4-4，得出BP=AB-AP=4cm=BC，由HL证明Rt△BCD≌Rt△BPD即可；
（2）当S△APD=3S△BPD时，AP=3BP，由题意得出方程，解方程即可．

（1）证明：如图1所示：

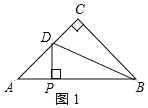
∵在RI△ABC中，∠C=90°，AC=BC=4cm，

∴AB=AC=4cm，

当t=（4-2）s时，AP=（4-2）=4-4，

∴BP=AB-AP=4cm，

∴BP=BC，

∵PD⊥AB，

∴∠BFD=∠C=90°，

在Rt△BCD和Rt△BPD中，，

∴Rt△BCD≌Rt△BPD（HL）；

（2）解：如图2所示：

∵PD⊥AB，当S△APD=3S△BPD时，AP=3BP，

即t=3（4-t），

解得：t=3，

∴当t为3s时，S△APD=3S△BPD．