题目内容
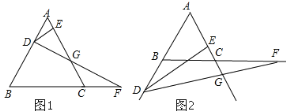
【题目】在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是
是![]() 上的一动点(不与点
上的一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 填空:①当
填空:①当![]() ________时,四边形
________时,四边形![]() 是矩形;②当
是矩形;②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
【答案】(1)详见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)利用菱形的性质和已知条件可证明四边形AMDN的对边平行且相等即可;
(2)①有(1)可知四边形AMDN是平行四边形,利用有一个角为直角的平行四边形为矩形即∠DMA=90°,所以AM=![]() AD=1时即可;
AD=1时即可;
②当平行四边形AMND的邻边AM=DM时,四边形为菱形,利用已知条件再证明三角形AMD是等边三角形即可.
(1)∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
又∵点E是AD边的中点,
∴DE=AE,
∴△NDE≌△MAE,
∴ND=MA,
∴四边形AMDN是平行四边形;
(2)①当AM的值为1时,四边形AMDN是矩形.理由如下:
∵四边形ABCD是菱形,
∴AB=AD=2.
∵AM=![]() AD=1,
AD=1,
∴∠ADM=30°
∵∠DAM=60°,
∴∠AMD=90°,
∴平行四边形AMDN是矩形;
故答案为:1;
②当AM的值为2时,四边形AMDN是菱形.理由如下:
∵AM=2,
∴AM=AD=2,
∴△AMD是等边三角形,
∴AM=DM,
∴平行四边形AMDN是菱形,
故答案为:2.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】端午节放假期间,某学校计划租用![]() 辆客车送
辆客车送![]() 名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车
名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
甲种客车 | 乙种客车 | |
载客量(人/辆) |
|
|
租金(元/辆) |
|
|
(1)求出![]() (元)与
(元)与![]() (辆)之间函数关系式;
(辆)之间函数关系式;
(2)求出自变量的取值范围;
(3)选择怎样的租车方案所需的费用最低?最低费用多少元?
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.