题目内容
计算:
(1)
÷(
×
)
(2)
-
-2
(3)|-
|-
+(1-
)0+
(4)(
+2)(
-2)-(2
-1)2
(5)
+
-
+(
-1)0
(6)解方程:9(x-2)2=25.
(1)
| 24 |
| 6 |
| 18 |
(2)
| 12 |
|
|
(3)|-
| 2 |
| 8 |
| 3 |
| 1 | ||||
|
(4)(
| 3 |
| 3 |
| 3 |
(5)
|
| 3 | 64 |
| 3 | -
| ||
| 3 |
(6)解方程:9(x-2)2=25.
考点:实数的运算
专题:计算题
分析:(1)原式利用二次根式的乘除法则计算即可得到结果;
(2)原式各项化简后,合并即可得到结果;
(3)原式利用绝对值的代数意义,二次根式的性质,以及零指数幂法则计算即可得到结果;
(4)原式第一项利用平方差公式化简,第二项利用完全平方公式展开,合并即可得到结果;
(5)原式利用平方根,立方根以及零指数幂法则计算即可得到结果;
(6)方程变形后,利用平方根定义计算即可求出解.
(2)原式各项化简后,合并即可得到结果;
(3)原式利用绝对值的代数意义,二次根式的性质,以及零指数幂法则计算即可得到结果;
(4)原式第一项利用平方差公式化简,第二项利用完全平方公式展开,合并即可得到结果;
(5)原式利用平方根,立方根以及零指数幂法则计算即可得到结果;
(6)方程变形后,利用平方根定义计算即可求出解.
解答:解:(1)原式=
÷
=
;
(2)原式=2
-
-
=
-
;
(3)原式=
-2
+1+
-
=
-2
+1;
(4)原式=3-2-12-1+4
=4
-12;
(5)原式=
+4+
+1=6
;
(6)方程变形得:(x-2)2=
,
开方得:x-2=±
,
解得:x1=
,x2=
.
| 24 |
| 108 |
| ||
| 3 |
(2)原式=2
| 3 |
| ||
| 2 |
2
| ||
| 3 |
4
| ||
| 3 |
| ||
| 2 |
(3)原式=
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(4)原式=3-2-12-1+4
| 3 |
| 3 |
(5)原式=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
(6)方程变形得:(x-2)2=
| 25 |
| 9 |
开方得:x-2=±
| 5 |
| 3 |
解得:x1=
| 11 |
| 3 |
| 1 |
| 2 |
点评:此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
在-1.414,-
,
,
,
,3.142,2.121121112中,无理数的个数是( )
| 2 |
| 22 |
| 7 |
| π |
| 3 |
| ||
| 2 |
| A、2 | B、3 | C、4 | D、5 |
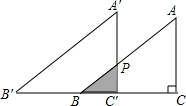 如图所示,在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm,若△A′B′C′与△ABC完全重合,令△ABC固定不动,将△A′B′C′沿CB所在的直线向左以1cm/s的速度移动.设移动xs后,△A′B′C′与△ABC的重合部分的面积为ycm2,求:
如图所示,在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm,若△A′B′C′与△ABC完全重合,令△ABC固定不动,将△A′B′C′沿CB所在的直线向左以1cm/s的速度移动.设移动xs后,△A′B′C′与△ABC的重合部分的面积为ycm2,求: