题目内容
1．如图，在数轴上，A1，P两点表示的数分别是1，2，A1，A2关于点O对称，A2，A3关于点P对称，A3，A4关于点O对称，A4，A5关于点P对称…依此规律，点A2015表示数是4029．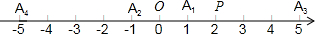
分析 根据对称性质，由题意找出数字的变化规律，确定出点A2015表示的数即可．
解答 解：根据对称的性质得：A2表示的数为-1，
A3表示的数为5，
A4表示的数为-5，
A5表示的数为9，
A6表示的数为-9，
A7表示的数为13，
A8表示的数为-13，
A9表示的数为17，
A10表示的数为-17，
A11表示的数为21，
…
可以看出当n为偶数时An表示的数为-2n+3；当n为奇数时An表示的数为2n-1；
则A2015表示的数是2×2015-1=4029．
故答案为：4029．
点评 此题考查了数轴，熟练掌握对称的性质是解本题的关键，从简单情形入手，找出规律解决问题．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
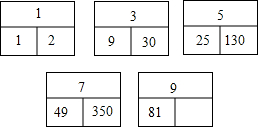
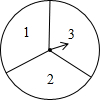2015年1月9日，2014年度国家科学技术奖励大会在北京人民大会堂举行．为了加强青少年科技创新的意识，某市举办了科学表演大赛．小丽和小红想利用转转盘的游戏决定谁去参加该大赛，游戏规则如下：如图是一个可以自由转动的转盘，被平均分成3个扇形，扇形上分别标有数字1，2，3，转动一次转盘，任其自由停止，指针会指向某个扇形（若指针指在分界线上，则重转），相应地得到一个数字，两人各转动一次，若得到的两个数字之和为偶数，则小丽去参赛，否则小红去参赛．