题目内容
已知等腰三角形一腰上的中线将三角形周长分成2:1两部分,已知三角形底边长为5cm,则腰长为 cm.
考点:等腰三角形的性质,三角形三边关系
专题:
分析:本题可分别设出等腰三角形的腰长,然后根据一腰上的中线所分三角形两部分的周长列出方程,进而可求得等腰三角形的腰长.注意此题一定要分为两种情况讨论,最后还要看所求的结果是否满足三角形的三边关系.
解答:解:设该三角形的腰长是xcm.根据题意,得:
x+
x=
(2x+5)或5+
x=
(2x+5),
解得,x=2,或x=20,
经检验,x=2不符合三角形的三边关系,
所以,等腰三角形的腰长为20cm,
故答案为20.
x+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解得,x=2,或x=20,
经检验,x=2不符合三角形的三边关系,
所以,等腰三角形的腰长为20cm,
故答案为20.
点评:本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确2:1两部分是哪一部分含有底边,所以一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
相关题目
 小强、小红俩兄妹是香市中学的学生,某天,兄妹俩决定比比看谁先到家,小强让小红先走,图中两条线段分别表示小强,小红回家过程中离学校的距离S(米)以及回家所用的时间T(分)的关系,请根据图象回答:
小强、小红俩兄妹是香市中学的学生,某天,兄妹俩决定比比看谁先到家,小强让小红先走,图中两条线段分别表示小强,小红回家过程中离学校的距离S(米)以及回家所用的时间T(分)的关系,请根据图象回答: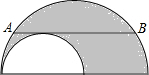 如图,大圆的弦AB与小圆相切,且小圆圆心在大圆直径上,若AB=12,则图中阴影部分的面积为
如图,大圆的弦AB与小圆相切,且小圆圆心在大圆直径上,若AB=12,则图中阴影部分的面积为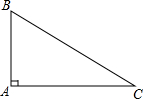 如图,在△ABC中,AB⊥AC,垂足为A.
如图,在△ABC中,AB⊥AC,垂足为A.