题目内容
1. 证明:三角形中位线定理.
证明:三角形中位线定理.已知:如图,D,E分别是△ABC的边AB,AC的中点.
求证:DE∥BC,DE=$\frac{1}{2}$BC.
证明:
分析 延长DE至点F,使EF=DE连接CF,根据SAS定理得出△ADE≌△CFE,故可得出四边形BCFD是平行四边形,据此可得出结论.
解答 求证:DE∥BC,DE=$\frac{1}{2}$BC. 证明:延长DE至点F,使EF=DE连接CF.
证明:延长DE至点F,使EF=DE连接CF.
∵E是AC的中点,
∴AE=CE.
在△ADE与△CFE中,
∵$\left\{\begin{array}{l}{DE=EF}\\{∠AED=∠CEF}\\{AE=CE}\end{array}\right.$,
∴△ADE≌△CFE(SAS),
∴AD=CF,∠ADE=∠F,
∴BD∥CF,
∴四边形BCFD是平行四边形,
∴DF∥BC,DF=BC,
∴DE∥BC,DE=$\frac{1}{2}$BC.
故答案为:DE∥BC,DE=$\frac{1}{2}$BC.
点评 本题考查的三角形中位线定理,根据题意作出辅助线,构造出平行四边形是解答此题的关键.

练习册系列答案
相关题目
12.某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如下表:
根据上表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
| A. | 该班一共有40名同学 | |
| B. | 该班学生这次考试成绩的众数是28分 | |
| C. | 该班学生这次考试成绩的中位数是28分 | |
| D. | 该班学生这次考试成绩的平均数是28分 |
16.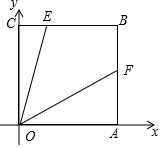 如图,在正方形OABC中,点B的坐标是(3,3),点E,F分别在边BC,BA上,CE=1,若∠EOF=45°,则F点的纵坐标是( )
如图,在正方形OABC中,点B的坐标是(3,3),点E,F分别在边BC,BA上,CE=1,若∠EOF=45°,则F点的纵坐标是( )
 如图,在正方形OABC中,点B的坐标是(3,3),点E,F分别在边BC,BA上,CE=1,若∠EOF=45°,则F点的纵坐标是( )
如图,在正方形OABC中,点B的坐标是(3,3),点E,F分别在边BC,BA上,CE=1,若∠EOF=45°,则F点的纵坐标是( )| A. | 1 | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
11. 将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
 将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )| A. | 136° | B. | 138° | C. | 140° | D. | 142° |
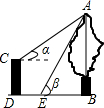 如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB=$\frac{3\sqrt{3}+12}{2}$(结果保留根号)
如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB=$\frac{3\sqrt{3}+12}{2}$(结果保留根号)