题目内容
11.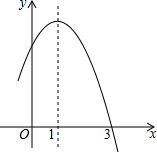 二次函数y=ax2+bx+c的函数图象如图所示,下列说法正确的个数为( )
二次函数y=ax2+bx+c的函数图象如图所示,下列说法正确的个数为( )①a<0;②b>0;③c=a;④b2-4ac>0;⑤4a-2b+c>0.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据图象得出a>0,-$\frac{b}{2a}$>0,c>0,结合图象上的点和对称轴即可逐项判断.
解答 解:∵二次函数的图象的开口向下,
∴a<0,①正确;
∵二次函数图象的对称轴是直线x=1,
∴-$\frac{b}{2a}$=1,
∴2a+b=0,b>0,②正确;
∵二次函数的图象y轴的交点在y轴的正半轴上,
∴c>0,
∵a<0,
∴a≠c,③错误;
∵二次函数的图象与x轴有两个交点,
∴b2-4ac>0,
∴④正确;
∵二次函数图象的对称轴是直线x=1,
∴抛物线上x=-1时的点与当x=3时的点对称,
即当x=-2时,y<0,
∴4a-2b+c<0故⑤错误.
故选B.
点评 本题主要考查了二次函数图象与系数的关系,解题的关键是会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
1. 如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )
如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )
 如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )
如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )| A. | $\frac{4}{3}$ | B. | 3 | C. | 5 | D. | $\frac{27}{4}$ |
19. 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )| A. | 4.8m | B. | 6.4m | C. | 8m | D. | 10m |
16.某工厂用12万元购进一台机器,随着使用年限的增加,机器的实际价值降低,机器的实际价值y(单位:万元)与使用年限x的关系如下表:
(1)写出实际价值y与年限x的关系;
(2)计算8年后该机器的实际价值;
(3)若机器的实际价值降到3万元时.就必须报废处理,计算这台机器可以使用多少年?
| 年限x | 1 | 2 | 3 | 4 |
| 实际价值y(万元) | 12-0.6 | 12-1.2 | 12-1.8 | 12-2.4 |
(2)计算8年后该机器的实际价值;
(3)若机器的实际价值降到3万元时.就必须报废处理,计算这台机器可以使用多少年?
20.下列计算正确的是( )
| A. | (-$\frac{3}{2}$)-1=$\frac{3}{2}$ | B. | $\frac{1}{a}+\frac{1}{b}=\frac{2}{a+b}$ | C. | $\frac{{a}^{2}-{b}^{2}}{a-b}=a+b$ | D. | (-$\frac{1}{20}$)0=0 |