题目内容
 某汽车租赁公司对某款汽车的租赁方式按时段计费,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还.租赁费用y(元)随时间x(天)的变化图象为折线OA-AB-BC,如图所示.
某汽车租赁公司对某款汽车的租赁方式按时段计费,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还.租赁费用y(元)随时间x(天)的变化图象为折线OA-AB-BC,如图所示.(1)当租赁时间不超过3天时,求每日租金.
(2)当6≤x≤9时,求y与x的函数解析式.
(3)甲、乙两人租赁该款汽车各一辆,两人租赁时间一共为9天,甲租的天数少于3天,乙比甲多支付费用720元.请问乙租这款汽车多长时间?
考点:一次函数的应用
专题:
分析:(1)根据函数图象由总租金÷租期就可以得出每天的租金;
(2)直接运用待定系数法就可以求出y与x之间的函数关系式;
(3)设乙租这款车a天,就有甲租用的时间为(9-a)天,分别表示出甲乙的租金从而建立方程求出其解即可.
(2)直接运用待定系数法就可以求出y与x之间的函数关系式;
(3)设乙租这款车a天,就有甲租用的时间为(9-a)天,分别表示出甲乙的租金从而建立方程求出其解即可.
解答:解:(1)由函数图象,得
450÷3=150元;
(2)设BC的解析式为y=kx+b,由函数图象,得
,
解得:
,
∴y与x之间的函数关系式为:y=210x-450(6≤x≤9);
(3)设乙租这款车a(a<3)天,就有甲租用的时间为(9-a)天,由题意,得
∴甲的租金为150(9-a),
乙的租金为210a-450,
∴210a-450-150(9-a)=720,
解得:a=7.
答:乙租这款汽车的时间是7天.
450÷3=150元;
(2)设BC的解析式为y=kx+b,由函数图象,得
|
解得:
|
∴y与x之间的函数关系式为:y=210x-450(6≤x≤9);
(3)设乙租这款车a(a<3)天,就有甲租用的时间为(9-a)天,由题意,得
∴甲的租金为150(9-a),
乙的租金为210a-450,
∴210a-450-150(9-a)=720,
解得:a=7.
答:乙租这款汽车的时间是7天.
点评:本题考查了单价=总价÷数量的运用,待定系数法求一次函数的解析式的运用,列一元一次方程解实际问题的运用,解答时三个问题是递进关系,必须依次解决每个问题才能求出最后一个问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
两列数如下:
7,10,13,16,19,22,25,28,31,…
7,11,15,19,23,27,31,35,39,…
第1个相同的数是7,第10个相同的数是( )
7,10,13,16,19,22,25,28,31,…
7,11,15,19,23,27,31,35,39,…
第1个相同的数是7,第10个相同的数是( )
| A、115 | B、127 |
| C、139 | D、151 |

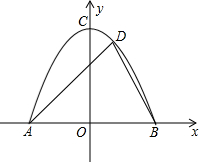 某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-
某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-