题目内容
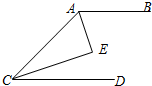 如图AB∥CD,AE,CE分别平分∠BAC,∠ACD,那么∠AEC=________度.
如图AB∥CD,AE,CE分别平分∠BAC,∠ACD,那么∠AEC=________度.
90
分析:根据平行线的性质得∠BAC+∠DCA=180°,再根据角平分线的定义得∠EAC= ∠BAC,∠ECA=
∠BAC,∠ECA= ∠DCA,则∠EAC+∠ECA=90°,然后根据三角形内角和定理可计算出∠AEC.
∠DCA,则∠EAC+∠ECA=90°,然后根据三角形内角和定理可计算出∠AEC.
解答:∵AB∥CD,
∴∠BAC+∠DCA=180°,
∵AE,CE分别平分∠BAC,∠ACD,
∴∠EAC= ∠BAC,∠ECA=
∠BAC,∠ECA= ∠DCA,
∠DCA,
∴∠EAC+∠ECA= (∠BAC+∠DCA)=90°,
(∠BAC+∠DCA)=90°,
∴∠AEC=90°.
故答案为90.
点评:本题考查了平行线的性质:两直线平行,同旁内角互补.也考查了角平分线的定义.
分析:根据平行线的性质得∠BAC+∠DCA=180°,再根据角平分线的定义得∠EAC=
 ∠BAC,∠ECA=
∠BAC,∠ECA= ∠DCA,则∠EAC+∠ECA=90°,然后根据三角形内角和定理可计算出∠AEC.
∠DCA,则∠EAC+∠ECA=90°,然后根据三角形内角和定理可计算出∠AEC.解答:∵AB∥CD,
∴∠BAC+∠DCA=180°,
∵AE,CE分别平分∠BAC,∠ACD,
∴∠EAC=
 ∠BAC,∠ECA=
∠BAC,∠ECA= ∠DCA,
∠DCA,∴∠EAC+∠ECA=
 (∠BAC+∠DCA)=90°,
(∠BAC+∠DCA)=90°,∴∠AEC=90°.
故答案为90.
点评:本题考查了平行线的性质:两直线平行,同旁内角互补.也考查了角平分线的定义.

练习册系列答案
相关题目
 如图AB∥CD,AE,CE分别平分∠BAC,∠ACD,那么∠AEC=
如图AB∥CD,AE,CE分别平分∠BAC,∠ACD,那么∠AEC=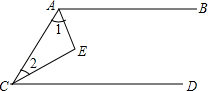 完成填空,如图AB∥CD,AE平分∠BAC,CE平分∠ACD.求证:AE⊥CE.
完成填空,如图AB∥CD,AE平分∠BAC,CE平分∠ACD.求证:AE⊥CE.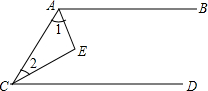 完成填空,如图AB∥CD,AE平分∠BAC,CE平分∠ACD.求证:AE⊥CE.
完成填空,如图AB∥CD,AE平分∠BAC,CE平分∠ACD.求证:AE⊥CE.