Question

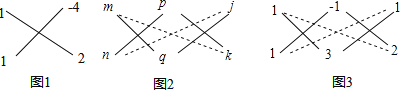
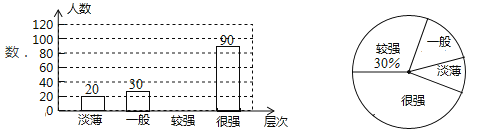
【题目】我国边防局接到情报，近海处有一可疑船只正向公海方向行驶，边防部迅速派出快艇追赶(如图1) ．图2中分别表示两船相对于海岸的距离 (海里)与追赶时间(分)之间的关系．根据图象问答问题：

（1）①直线与直线中 表示到海岸的距离与追赶时间之间的关系；

②与比较 速度快；

③如果一直追下去，那么________ (填 “能”或“不能")追上；

④可疑船只速度是 海里/分，快艇的速度是 海里/分；

（2）与对应的两个一次函数表达式与中的实际意义各是什么？并直接写出两个具体表达式．

（3）分钟内能否追上？为什么？

（4）当逃离海岸海里的公海时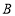，将无法对其进行检查，照此速度，能否在逃入公海前将其拦截？为什么？

Answer 1

【答案】（1）①;②;③能;④0.2,0.5.（2）两直线函数表达式中的表示的是两船的速度. A船:,B船:.（3）15分钟内不能追上.（4）能在逃入公海前将其拦截.

【解析】

（1）①根据图象的意义, 是从海岸出发, 表示到海岸的距离与追赶时间之间的关系;②观察两直线的斜率, B船速度更快; ③B船可以追上A船; ④根据图象求出两直线斜率,即为两船的速度.

（2）两直线函数表达式中的表示的是两船的速度.

（3）求出两直线的函数表达式,令时间,代入两表达式,若,则表示能追上,否则表示不能追上.

（4）联立两函数表达式,解出B船追上A船时的时间与位置,与12海里比较,若该位置小于12海里,则表示能在逃入公海前将其拦截.

解: （1）①直线与直线中, 表示到海岸的距离与追赶时间之间的关系；

②与比较, 速度快；

③B船速度更快,可以追上A船;

④B船速度海里/分;

A船速度海里/分.

（2）由图象可得,将点代入,

可得,解得,表示B船的速度为每分钟0.5海里,

所以:.

将点,代入,

可得,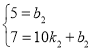

解得,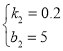

所以:,

表示A船速度为每分钟0.2海里.

（3）当时,

,

,

,所以15分钟内不能追上.

（4）联立两表达式,

,

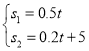解得,

此时,

所以能在逃入公海前将其拦截.