题目内容
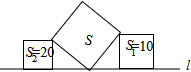 如图摆放的三个正方形,S表示面积,则S=( )
如图摆放的三个正方形,S表示面积,则S=( )| A、10 | B、500 |
| C、300 | D、30 |
考点:勾股定理,全等三角形的判定与性质,正方形的性质
专题:
分析:标注字母,根据正方形的性质可得AB=BC,根据同角的余角相等求出∠ABE=∠BCF,再利用“角角边”证明△ABE和△BCF全等,根据全等三角形对应边相等可得AE=BF,再根据勾股定理可得S=S1+S2.
解答: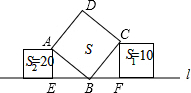 解:如图,∵四边形ABCD是正方形,
解:如图,∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=90°,
∵∠CBF+∠BCF=90°,
∴∠ABE=∠BCF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴AE=BF,
由勾股定理得,CF2+BF2=BC2,
∴S=S1+S2=10+20=30.
故选D.
 解:如图,∵四边形ABCD是正方形,
解:如图,∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=90°,
∵∠CBF+∠BCF=90°,
∴∠ABE=∠BCF,
在△ABE和△BCF中,
|
∴△ABE≌△BCF(AAS),
∴AE=BF,
由勾股定理得,CF2+BF2=BC2,
∴S=S1+S2=10+20=30.
故选D.
点评:本题考查了勾股定理,全等三角形的判定与性质,正方形的性质,标注字母并求出两个三角形全等是解题的关键.

练习册系列答案
相关题目
方程2x+3y=7的正整数解有( )
| A、无数个 | B、2个 | C、1个 | D、0个 |
某市有7500名学生参加中考,为了了解考试情况,从中抽取1000名学生的成绩进行统计分析,在这个问题中,有以下说法:
①1000名考生是总体的一个样本;
②1000名考生的平均成绩可估计总体平均成绩;
③7500名考生是总体;
④样本容量是1000.
其中正确的说法有( )
①1000名考生是总体的一个样本;
②1000名考生的平均成绩可估计总体平均成绩;
③7500名考生是总体;
④样本容量是1000.
其中正确的说法有( )
| A、1种 | B、2种 | C、3种 | D、4种 |
在平面坐标系内,点A位于第二象限,距离x轴1个单位长度,距离y轴4个单位长度,则点A的坐标为( )
| A、(1,4) |
| B、(-4,1) |
| C、(-1,-4) |
| D、(4,-1) |
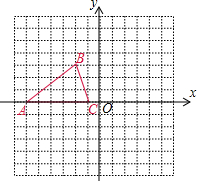 如图,已知△ABC的三个顶点的坐标分别为A(-6,0)、B(-2,3)、
如图,已知△ABC的三个顶点的坐标分别为A(-6,0)、B(-2,3)、