题目内容
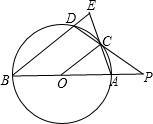
已知：P为⊙O外一点，PQ切⊙O于Q，PAB、PCD是⊙O的割线，且∠PAC=∠BAD．求证：PQ2-PA2=AC•AD．分析：由切割线定理得PQ2=PA•PB，可将PQ2-PA2变形为PA•AB，根据圆内接四边形的性质得∠PCA=∠B，已知∠PAC=∠BAD，可证△PAC∽△DAB，得
=
，即PA•AB=AC•AD，证明结论．
| PA |
| AD |
| AC |
| AB |
解答：
证明：如图，∵PQ为⊙O的切线，PAB为⊙O的割线，
由切割线定理，得PQ2=PA•PB，
∴PQ2-PA2=PA•PB-PA2=PA（PB-PA）=PA•AB，
由圆内接四边形的性质，得∠PCA=∠B，又∠PAC=∠BAD，
∴△PAC∽△DAB，
∴
=
，
即PA•AB=AC•AD，
∴PQ2-PA2=AC•AD．
证明：如图，∵PQ为⊙O的切线，PAB为⊙O的割线，由切割线定理，得PQ2=PA•PB，
∴PQ2-PA2=PA•PB-PA2=PA（PB-PA）=PA•AB，
由圆内接四边形的性质，得∠PCA=∠B，又∠PAC=∠BAD，
∴△PAC∽△DAB，
∴
| PA |
| AD |
| AC |
| AB |
即PA•AB=AC•AD，
∴PQ2-PA2=AC•AD．
点评：本题考查了切割线定理、圆内接四边形的性质，相似三角形的判定与性质的运用．关键是根据题意，找到证题的突破口．
练习册系列答案
相关题目
如图，已知：P为⊙O外一点，过P作⊙O的两条割线，分别交⊙O于A、B和C，D，且AB是⊙O的直径，弧AC=弧DC，连接BD，AC，OC．