题目内容
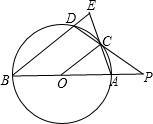如图，已知：P为⊙O外一点，过P作⊙O的两条割线，分别交⊙O于A、B和C，D，且AB是⊙O的直径，弧AC=弧DC，连接BD，AC，OC．（1）求证：OC∥BD；
（2）如果PA=AO=4，延长AC与BD的延长线交于E，求DE的长．
分析：（1）根据圆周角定理及平行线的判定进行分析即可；
（2）由已知可求得OB的长，根据OC∥BD易证△PCO∽△PDB，△ACO∽△AEB，利用其相似比即可求出DE的长．
（2）由已知可求得OB的长，根据OC∥BD易证△PCO∽△PDB，△ACO∽△AEB，利用其相似比即可求出DE的长．
解答：（1）证明：∵
=
∴
=2
∴∠COA=∠ABD
∴OC∥BD；
（2）解：∵PA=AO=4，OA为⊙O的半径
∴OB=4
又∵OC∥BD
∴△PCO∽△PDB
∴
=
∴
=
∴BD=6
同理可得BE=8
∴DE=BE-BD=8-6=2．
 |
| AC |
|
| DC |
∴
|
| AD |
|
| AC |
∴∠COA=∠ABD
∴OC∥BD；
（2）解：∵PA=AO=4，OA为⊙O的半径
∴OB=4
又∵OC∥BD
∴△PCO∽△PDB
∴
| OP |
| BP |
| OC |
| BD |
∴
| 8 |
| 8+4 |
| 4 |
| BD |
∴BD=6
同理可得BE=8
∴DE=BE-BD=8-6=2．
点评：本题考查的是圆周角定理及相似三角形的性质的综合运用．
练习册系列答案
金钥匙试卷系列答案
相关题目
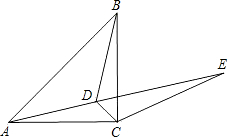如图，已知点D为等腰直角△ABC内一点，∠CAD=∠CBD=15°．
如图，已知在半径为2的⊙O中有一点E，过点E的弦AB与CD互相垂直，且OE=1，则AB2+CD2的值等于
如图，已知点D为△ABC中AC边上一点，且AD：DC=3；4，设
如图，已知：△ABC为直角三角形，∠B=90°，AB垂直x轴，M为AC中点．若A点坐标为（3，4），M点坐标为（-1，1），则B点坐标为（ ）
角度后得到△ADF，延长BE交DF于点G，且AF=4，AB=7．