Question

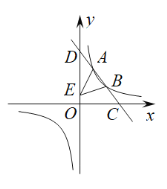
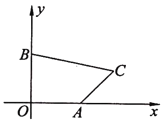
【题目】如图，在平面直角坐标系中，点，，的坐标分别为，，，一直线经过点将四边形分割成两块，这两块的面积比为1：2，则该直线的表达式为________．

Answer 1

【答案】或

【解析】

过点C作CD⊥x轴于点D，过点C作直线CE交y轴于点E，过点C作直线CF交y轴于点F，先求出四边形的面积，再分两种情况：①当时，②当时，分别求出该直线的解析式，即可．

过点C作CD⊥x轴于点D，过点C作直线CE交y轴于点E，过点C作直线CF交y轴于点F，

∵点，，的坐标分别为，，，

∴CD=2，OB=3，OD=5,AD=2，

∴四边形的面积=．

①当时，则，

∴BE=3.5×2÷5=，

∴OE=3-=

即：E(0，)，

设直线CE的解析式为：y=kx+b，

把E(0，)，C代入得：，解得：，

∴直线CE的解析式为：；

②当时，则，

∴BF=7×2÷5=，

∴OF=3-=，

即：F(0，)，

∴直线CF的解析式为：．

综上所述：该直线的表达式为：或．

故答案是：或．