题目内容
15．
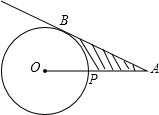如图，已知A为⊙O外一点，连接OA，交⊙O于P，AB是⊙O的切线，B是切点，且PO=2cm，AB=2$\sqrt{3}$cm，求阴影部分的面积．
分析 阴影部分的面积=三角形的面积-扇形的面积．依据面积公式计算即可．
解答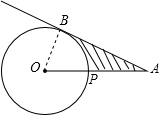 
解：连接OB，
∵AB是⊙O的切线，B是切点，
∴∠ABO=90°，
∵OB=PO=2cm，AB=2$\sqrt{3}$cm，
∴tan∠AOB=$\frac{AB}{OB}$=$\sqrt{3}$，
∴∠AOB=60°，
从图中可以看出阴影部分的面积=S△AOB-S扇形OBP=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{60π×{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2}{3}$π（cm2）．
点评 本题主要考查了切线的性质及扇形的面积公式．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
经过两个已知点A、B能确定一个圆吗？经过两个已知点A、B所作的圆的圆心在怎样的一条直线上？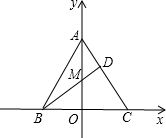
在平面直角坐标系中，已知A点在y轴正半轴上，B点在x轴负半轴上，C点在x轴正半轴上，BD是△ABC的高，且交y轴于点M．