题目内容
16.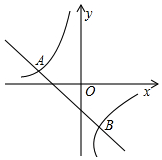 如图,已知一次函数与反比例函数y=$\frac{k}{x}$的图象相交于点 A(-3,1)和点B(a,-3)
如图,已知一次函数与反比例函数y=$\frac{k}{x}$的图象相交于点 A(-3,1)和点B(a,-3)(1)求反比例函数的表达式;
(2)求点B的坐标及一次函数的表达式;
(3)观察图象,直接写出反比例函数数值大于一次函数数值时对应x的取值范围.
分析 (1)直接把点A(-3,1)代入反比例函数y=$\frac{k}{x}$,求出k的值即可;
(2)把点B(a,-3)代入反比例函数的解析式即可得出a的值,进而得出B点坐标,再用待定系数法求出直线AB的解析式即可;
(3)直接根据一次函数与反比例函数的交点坐标即可得出结论.
解答 解:(1)∵点A(-3,1)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=1×(-3)=-3,
∴反比例函数的解析式为:y=-$\frac{3}{x}$;
(2)∵点B(a,-3)在反比例函数y=-$\frac{3}{x}$的图象上,
∴-$\frac{3}{a}$=-3,解得a=1,
∴B(1,-3).
设直线AB的解析式为y=ax+b(a≠0),
∵A(-3,1),B(1,-3),
∴$\left\{\begin{array}{l}{-3a+b=1}\\{a+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$,
∴一次函数的表达式为:y=-x-2;
(3)由函数图象可知,当-3<x<1时,反比例函数数值大于一次函数数值.
点评 本题考查的是反比例函数与一次函数的交点问题,能直接利用函数图象求出不等式的解集是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 如图,小手盖住的点的坐标可能是( )
如图,小手盖住的点的坐标可能是( )
 如图,小手盖住的点的坐标可能是( )
如图,小手盖住的点的坐标可能是( )| A. | (1,-1) | B. | (2,2) | C. | (-3,-3) | D. | (-3,4) |
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
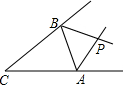 如图,△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于P.求证:点P到三边AB,BC,CA所在的直线的距离相等.
如图,△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于P.求证:点P到三边AB,BC,CA所在的直线的距离相等. 如图,将△ABC沿CB方向平移3cm到△A′B′C′的位置,若BC=5cm,则B′C=8cm.
如图,将△ABC沿CB方向平移3cm到△A′B′C′的位置,若BC=5cm,则B′C=8cm. ”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
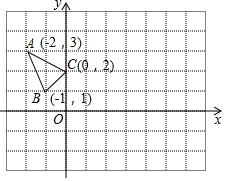 △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示. 如图,在Rt△ABC中,斜边AB的垂直平分线交AC于点D,交AB于点E,∠CBD=26°,则∠A=32度.
如图,在Rt△ABC中,斜边AB的垂直平分线交AC于点D,交AB于点E,∠CBD=26°,则∠A=32度.